2014-02-02
404
Приведем без доказательства основные свойства преобразования Фурье. Введем обозначения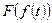 
– преобразования Фурье функции f(t).
1. Свойство линейности: если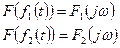 
, то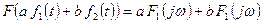 
.
2. Свойство изменения масштаба: если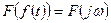 
, то для любой действительной постоянной а преобразования Фурье: 
.
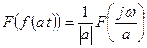3. Свойство частотного сдвига: если 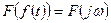, то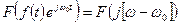 
Следствие из 3 свойства:
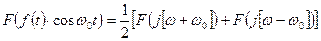
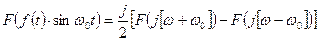
4. Свойство временного сдвига: если 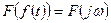, то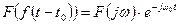 
.
5. Дифференцирование и интегрирование во времени: если 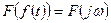, то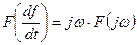 
; 
.
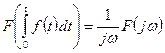6. Теорема о свертке: есл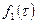и 
и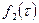 
, т.е. 
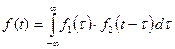(это свертка), то преобразование Фурье от 
: 
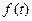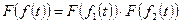(в частотной области).
7. Теорема произведения: если ,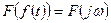 
, 
, 
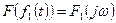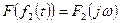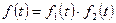, то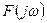 
представляет собой свертку спектров 
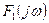и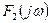 
, т.е. 
(
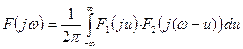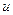имеет размерность частоты).
Замечание:
Если в качестве аргументов спектральной плотности фигурирует не круговая, а обычная частота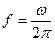 
, то множитель 
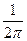в последнем выражении отсутствует.
