Параграф 1.9.2: Вероятностное описание случайного процесса

Рассмотрим N реализаций случайных процессов X(t). Для общности рассуждений будем рассматривать непрерывный случайный процесс. Выделим из этого числа те n₁ реализаций, значения в определенный момент времени t₁ не превышают некоторого числа х₁. При достаточно большом числе N относительная доля 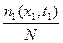функций, находящихся в момент t₁ не выше уровня х₁, будет обладать статистической устойчивостью, т.е. будет оставаться приблизительно постоянным числом. Это число определяет вероятность того, что при t=t₁ случайная функция x(t) не превышает уровень х₁, и обозначается 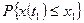. Указанная вероятность зависит от фиксированного момента времени t₁ и от выбранного уровня х₁, т.е. является функцией двух переменных. Это функция 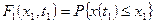называется одномерной интегральной функцией распределения случайного процесса 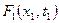в некотором сечении t₁ при каждом значении своего аргумента x₁ численно равно вероятности того, что реализация сечения процесса x (t₁) не превышает уровня значения х₁. Вероятностные из N реализаций те n₁, которые попадают в некоторый интервал 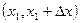. При большом N относительная доля 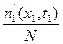функций, попадающих в этот интервал, так же будет оставаться приблизительно постоянной, и определяет вероятность того, что при t=t₁ случайная величина x (t₁) будет находиться внутри интервала 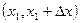, и обозначим это как:

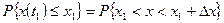
Очевидно, что при происходит следующее:

1. рассматриваемая вероятность превращается в вероятность того, что x (t₁) = х₁, т.е.

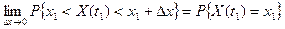
2.

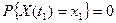
Однако, если рассматривать функцию

,

то при каждом значении x₁ она будет конечной и позволит охарактеризовать плотность распределения вероятностей возможных значений х₁. Нетрудно показать, что 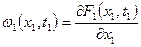. Поэтому 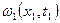называют одномерной дифференциальной функцией распределения, или плотностью распределения вероятностей.

Более полно свойство случайного процесса можно охарактеризовать, если для любого набора n моментов времени t₁, t₂, …, t_n и любых значений x₁, x₂, …, x_n вычислить вероятность того, что X (t) принимает в указанные моменты времени значения, не превышающие значения x₁, x₂, …, x_n.

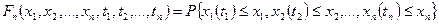
Функция 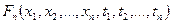называется n-мерной интегральной функций распределения вероятностей процесса X (t). Если существует частная производная n -мерной интегральной функции распределения по всем x_k (k = 0, …, n), то можно определить n -мерную плотность распределения вероятности:

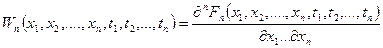
по которой так же можно определить процесс. Т.о., вероятностные свойства случайного процесса можно охарактеризовать с помощью n -мерной функции распределения (интегральной или дифференциальной) тем полнее, чем больше n. При этом, если мы имеем финитный случайный процесс, дискретный по времени, или дискретный и по уровню и по времени (1 – случайная последовательность, 2 – дискретный случайный процесс), представляющий собой конечный отрезок последовательности, содержащий n отсчетов, то n-мерная функция распределения дает исчерпывающее вероятностное описание этого процесса или представляет собой его полную вероятностную модель. Для непрерывных во времени процессов полной вероятностной моделью является бесконечно-мерная функция распределения, определить которую в принципе невозможно. Однако, если ширина спектра такого процесса ограничена сверху частотой f_n, то в соответствие с теоремой Котельникова, каждую реализацию случайной функции длительностью Т можно полностью определить дискретной выборкой, содержащей 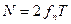отсчетов, следующих с интервалом 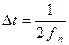. В этом случае, непрерывные случайные процессы можно так же с высокой точностью определить n -мерным законом распределения.