2014-02-02
545
Стационарные в широком смысле процессы в большинстве практически важных ситуаций обладают так называемым эргодическим свойством (усреднение по множеству реализаций случайного процесса x(t) дает примерно тот же результат, что и усреднение по времени одной реализации x(t), если время усреднения Т достаточно велико). Достаточное условие эргодичности стационарного в широком смысле процесса можно записать в виде:
(*)
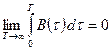Математическое ожидание для эргодического процесса можно определить путем усреднения по времени (обозначается волнистой чертой сверху) единственной реализации x(t):
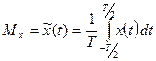
Т.о., для эргодического процесса нахождение Математического ожидания сводится к интегрированию одной реализации процесса.
Дисперсия эргодического процесса можно найти так:
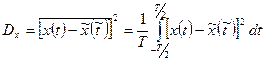
Эта величина представляет собой среднюю мощность переменной составляющей процесса:
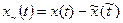
Здесь операция определения дисперсии сводится к операции возведения в квадрат переменной составляющей процесса и интегрирования. Функция корреляции эргодического случайного процесса также можно получить усреднением по времени:
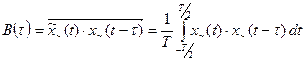
Очевидно, что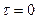 
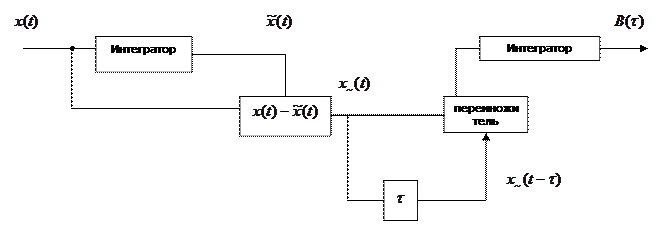
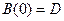. Схема измерения функции корреляции согласно этому алгоритму имеет вид:
Графики типовых функций корреляции:
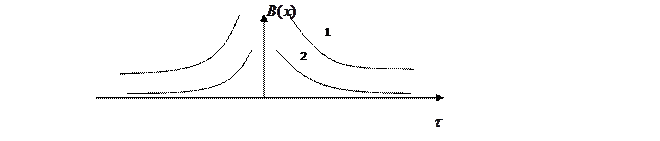
У кривой 1 корреляционная связь медленно убывает, а 2 кривой – быстрее. Коэффициент и функция корреляции для эргодического случайного процесса стремится к 0 с увеличением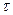 
. Это происходит потому, что чем дольше отстоят друг от друга сечения, то тем слабее статистическая зависимость между ними. Интервал времени 
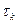называется временем корреляции процесса, если при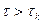 
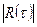становится пренебрежительно малой (практически, в большинстве случаев достаточно, чтобы она стала меньше 0.1) Время корреляции обычно определяют как основание прямоугольного прямоугольника с высотой, равной 1, площадь которого равна площади ограниченной кривой 
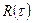и осями координат.
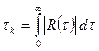
Можно показать, что достаточное условие эргодичности стационарности в широком смысле процесса (*) эквивалентно условию:
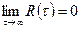
Данное условие позволяет трактовать физический смысл эргодической гипотезы т.о.: при его выполнении отдаленные более чем на 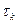отрезки, рассматриваемые реализацией процесса, можно считать отдельными реализациями процесса в виду их слабой статистической взаимосвязи. Т.о., и появляется возможность замены усреднения ансамбля по времен (по ансамблю – по dx).
