2014-02-02
2722
Для описания случайных процессов наряду с корреляционными функциями широко используются спектральные характеристики, в частности, энергетический спектр (спектральная плотность мощности) 
. Для выяснения физического смысла этой величины проведем следующие рассуждения:
Реализация стационарного центрированного случайного процесса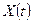 
в общем случае имеет бесконечную энергию, и, следовательно, не имеют преобразования Фурье.
Рассмотрим усеченный процесс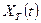 
, получающийся из исходного:
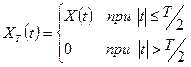
Реализация такого процесса ограничена во времени, следовательно, для них существуют преобразования Фурье.
В соответствие с равенством Парсеваля, для каждой реализации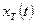 
этого процесса справедливо соотношение:
Равенство Парсеваля
где 
– преобразование Фурье реализации ;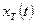
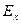– энергия сигнала.
Данное равенство показывает, что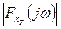 
характеризует распределение энергии реализации 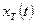по оси частот. Усреднив эту функцию по всем реализациям процесса, получим спектральную плотность энергию процесса 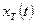. Найдем математическое ожидание:
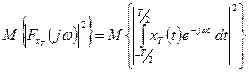
Оно определяет распределение энергии по частотам уже не одной реализации, а всего процесса 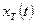. Однако с её использованием можно характеризовать лишь усеченный стационарный процесс 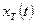, имеющий конечную энергию 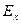. Для того чтобы получить характеристику не усеченного стационарного процесса 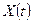, обладающего бесконечной 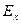, разделим спектральную плотность энергии 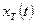на Т и устремим 
:
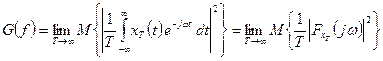
Полученная характеристика представляет собой спектральную плотность мощности стационарного процесса; определяет среднюю мощность, приходящуюся на 1 Гц на заданной частоте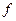
. При этом, мощность 
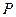обусловлена частотной составляющей в пределах очень узкой полосы 
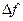вокруг средней частоты 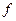будет равна:
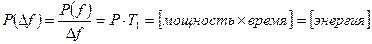
Поэтому эту характеристику часто называют также энергетическим спектром. Отметим некоторые свойства спектральной плотности мощности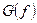 
:
1. из её определения следует, что она неотрицательна;
2. в отличие от обычной комплексной спектральной плотности, определенной преобразованием Фурье, энергетический спектр 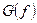не зависит от спектра фаз реализации процесса 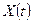, а однозначно определяется спектром амплитуд 
;
3. кривая, изображающая функцию 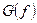, ограничивает вместе с осью абсцисс площадь, равную мощности процесса :
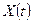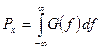
Как известно, для действительной функции 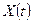модуль 
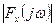является четной функцией частоты, поэтому л спектральной плотности мощности можно судить и по одной половине графика функции 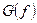, например, при 
.
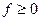В связи с этим вводят понятие односторонней спектральной плотности мощности, заданной при 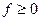, таким образом:
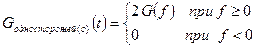
Множитель «2» в этой формуле обеспечивает равенство: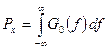 
. Нормированной спектральной плотностью мощности 
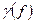или нормированным энергетическим спектром называют отношение:
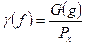
Площадь, ограничивающая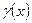 
и 0х, всегда равна 1.
Часто применяют математическую модель сигналов, у которых спектр отличен от 0 только в некоторой полосе частот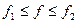 
, т.е. процессы с финитным спектром. Разность 
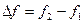называют шириной спектра. В реальных условиях жесткого ограничения не бывает, и ширину энергетического спектра определяют по различным критериям. Иногда под шириной спектра 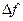понимают ширину минимальной полосы частот, в которой сосредоточена подавляющая часть (95%) мощности сигнала. Существует критерий эквивалентности прямоугольника, по которому эквивалентная ширина спектра определяется так:
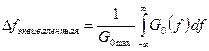
где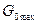 
– максимальное значение 
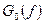в полосе частот случайного процесса.
Т.о.,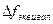 
– это основание прямоугольника с высотой 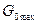, у которого такая же площадь, как у кривой энергетического спектра исследуемого процесса.
