Причиной автокорреляции остатков может быть либо неверная спецификация модели, либо наличие неучтенных факторов. Устранение этих причин не всегда дает нужные результаты. Автокорреляция остатков имеет собственные внутренние причины, связанные с автокорреляционной зависимостью.
Пусть исходное уравнение регрессии 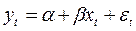 содержит автокорреляцию случайных членов.
содержит автокорреляцию случайных членов.
Допустим, что автокорреляция подчиняется автокорреляционной схеме первого порядка: 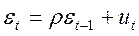 , где
, где 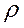 - коэффициент автокорреляции, а
- коэффициент автокорреляции, а 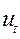 - случайный член, удовлетворяющий предпосылкам МНК.
- случайный член, удовлетворяющий предпосылкам МНК.
Данная схема оказывается авторегрессионой, поскольку 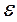 определяется значениями этой же величины с запаздыванием, и схемой первого порядка, потому что в этом случае запаздывание равно единице.
определяется значениями этой же величины с запаздыванием, и схемой первого порядка, потому что в этом случае запаздывание равно единице.
Величина 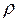 есть коэффициент корреляции между двумя соседними ошибками. Пусть
есть коэффициент корреляции между двумя соседними ошибками. Пусть 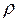 известно. Преобразуем исходное уравнение регрессии следующим образом:
известно. Преобразуем исходное уравнение регрессии следующим образом:
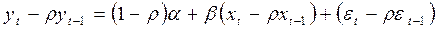 .
.
Обозначим: 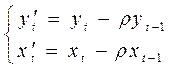 .
.
Это преобразование переменных называется авторегрессионым (AR), или преобразованием Бокса-Дженкинса.
Тогда преобразованное уравнение 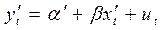 , где
, где 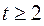 ,
, 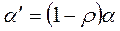 , не содержит автокорреляцию, и для оценки его параметров
, не содержит автокорреляцию, и для оценки его параметров 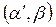 используется обычный МНК.
используется обычный МНК.
Способ вычисления 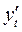 и
и 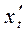 приводит к потере первого наблюдения. Эта проблема при малых выборках обычно преодолевается с помощью поправки Прайса-Винстена:
приводит к потере первого наблюдения. Эта проблема при малых выборках обычно преодолевается с помощью поправки Прайса-Винстена:
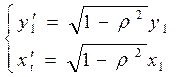
Оценка коэффициента 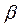 из этой зависимости непосредственно используется и для исходного уравнения, а коэффициент рассчитывается по формуле:
из этой зависимости непосредственно используется и для исходного уравнения, а коэффициент рассчитывается по формуле: 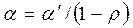 .
.
На практике величина 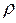 неизвестна, ее оценка получается одновременно с оценками
неизвестна, ее оценка получается одновременно с оценками 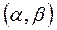 в результате следующих итеративных процедур.
в результате следующих итеративных процедур.
Процедура Кохрейна-Оркатта. Процедура включает следующие этапы:
1. Применяя МНК к исходному уравнению регрессии, получают первоначальные оценки параметров 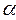 и
и 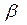 ;
;
2. Вычисляют остатки 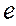 и в качестве оценки
и в качестве оценки 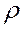 используют коэффициент автокорреляции остатков первого порядка, т.е. полугают
используют коэффициент автокорреляции остатков первого порядка, т.е. полугают 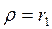 ;
;
3. Применяя МНК к преобразованному уравнению, получают новые оценки параметров 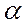 и
и 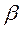 .
.
Процесс обычно заканчивается, когда очередное приближение 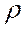 мало отличается от предыдущего. Процедура Кохрейна-Оркатта реализована в большинстве эконометрических компьютерных программах.
мало отличается от предыдущего. Процедура Кохрейна-Оркатта реализована в большинстве эконометрических компьютерных программах.
Процедура Хильдрата-Лу. Эта процедура, также широко применяема в регрессионных пакетах, основана на тех же самых принципах, но использует другой алгоритм вычислений:
1. Преобразованное уравнение оценивают для каждого значения 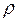 из интервала (-1;1) с заданным шагом внутри его;
из интервала (-1;1) с заданным шагом внутри его;
2. Выбирают значение 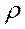 , для которого сумма квадратов остатков в преобразованном уравнении минимальна, а коэффициенты регрессии определяются при оценивании преобразованного уравнения с использованием этого значения.
, для которого сумма квадратов остатков в преобразованном уравнении минимальна, а коэффициенты регрессии определяются при оценивании преобразованного уравнения с использованием этого значения.
Пример 3. Воспользуемся данными примера 1.
Пусть исходная модель имеет вид:  .
.
По исходным данным с использованием МНК получено следующее оцененное уравнение регрессии:
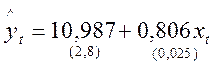 ,
, 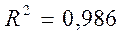
Коэффициент автокорреляции остатков первого порядка составляет 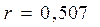 , следовательно, DW
, следовательно, DW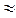 2(1-r) = 0,986. При уровне значимости 5% табличное значение
2(1-r) = 0,986. При уровне значимости 5% табличное значение 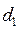 =1,106 и
=1,106 и 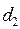 =1,371. Поскольку
=1,371. Поскольку 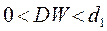 , то имеется положительная автокорреляция остатков.
, то имеется положительная автокорреляция остатков.
Применяя МНК к преобразованным данным: 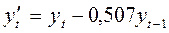 ,
, 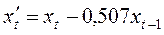 (
(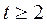 ), получим оценку преобразованного уравнения:
), получим оценку преобразованного уравнения:
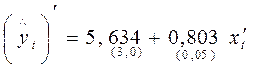 ,
, 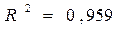 .
.
Коэффициент автокорреляции остатков первого порядка составляет 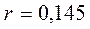 , следовательно, DW
, следовательно, DW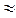 2(1-r) = 1,71. Поскольку
2(1-r) = 1,71. Поскольку 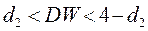 , то автокорреляция остатков отсутствует.
, то автокорреляция остатков отсутствует.
Пересчитывая оценку 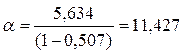 , получим следующую оценку исходной модели:
, получим следующую оценку исходной модели: 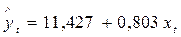 ,
, 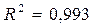 . Это уравнение отличается от полученного ранее уравнения, оцененного обычным МНК.
. Это уравнение отличается от полученного ранее уравнения, оцененного обычным МНК.
Приложение 1.
 2014-02-02
2014-02-02 1886
1886
