Аналитическое выравнивание временного ряда

Рассмотрим модель временного ряда y_t = f (t) + 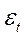, где f (t) - неслучайная составляющая (тренд, либо тренд и циклическая и (или) сезонная компонента, выражающая основную тенденцию).

Под выравниванием временного ряда понимают выделение неслучайной составляющей f (t), которая характеризует основную тенденцию изучаемого процесса, и выбор этой функции. Наиболее часто используются следующие функции:

f (t) = a + bt - линейная;

f (t) = a + b₁t + b₂t² + … + b_ntⁿ - полиномиальная;

f (t) = e^a+bt - экспоненциальная;

f (t) = a/(1 + be^-ct) - логистическая;

f (t) = C^a-b(r) - Кривая Гомперца, 0<r<1 и т.д.

Вид функции f (t) подбирается на основе графического изображения временного ряда с использованием содержательного анализа. Параметры каждого из видов функции f (t) можно определить обычным МНК, используя в качестве независимой переменной время t = 1,…,n, а в качестве зависимой – фактические значения уровней временного ряда.

Существует несколько способов определения типа тенденции:

1) анализ графического изображения ряда;

2) сравнение коэффициентов автокорреляции 1-го порядка, рассчитанных по исходным и преобразованным уровням ряда:

- если ряд имеет линейную тенденцию, то его соседние уровни y_t и y_t-1 тесно коррелируют r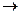(1) 1;

- если ряд содержит нелинейную тенденцию, то коэффициент автокорреляции r(1) первого порядка по логарифмам уровней исходного ряда будет выше, чем соответствующий коэффициент для уровней ряда.

Выбор лучшего уравнения осуществляют путем перебора основных форм и расчета по каждому уравнению R²_adj и выбора уравнения с максимальным R²_adj.

Например. Для предыдущего примера построим график временного ряда с помощью «Мастера диаграмм» и добавим линию тренда.

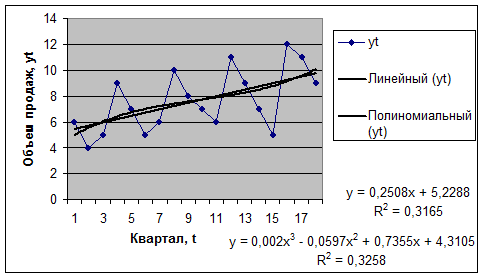
Отметим, что, как и раньше, наиболее простую экономическую интерпретацию имеют параметры линейного и экспоненциального трендов:

- линейный тренд: y_t = a + bt, a – начальный уровень временного ряда, b – средний абсолютный прирост уровней ряда. Система нормальных уравнений имеет вид

; ;

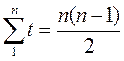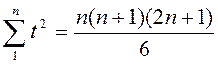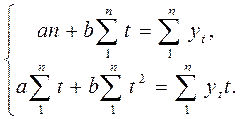
- экспоненциальный тренд: y_t = e ^{a +bt}, е ^а – начальный уровень временного ряда, е^b – средний в единицу времени коэффициент роста уровней ряда. Определение параметров требует предварительной линеаризации.

Другим методом выравнивания временного ряда является метод скользящей средней. Он основан на переходе от начальных значений членов ряда к их средним значениям на интервале времени, длина которого определена заранее. Получаемый т.о. ряд ведет себя более гладко, чем исходный из-за устранения отклонений ряда. Рассмотрим использование этого метода на примере построения аддитивной и мультипликативной моделей временного ряда с сезонной составляющей:

, .

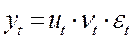(Если амплитуда колебаний приблизительно постоянна, то строят аддитивную модель, в противном случае – мультипликативную). Например, для рассматриваемого примера амплитуду можно считать приблизительно постоянной, следовательно подходящей будет аддитивная модель.

Процесс построения модели включает следующие шаги:

1. Выравнивание ряда методом скользящей средней.

2. Расчет значений сезонной составляющей .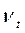

3. Устранение сезонной составляющей и получение выравненных данных 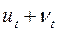или .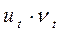

4. Аналитическое выравнивание уровне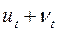й или 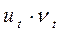и расчет значений .

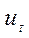5. Расчет полученных по модели значений 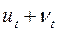или .

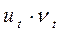6. Расчет абсолютных и (или) относительных ошибок.

Пояснения к выполнению шагов.

1. Проведем выравнивание исходных уровней ряда методом скользящей средней (таблица 1):

а) просуммируем уровни последовательно за каждые 4 квартала со сдвигом на один момент времени;

б) найдем скользящие средние делением на 4 полученных сумм (полученные значения уже не содержат сезонной компоненты);

в) приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих

средних – центрированные скользящие средние.

2. Оценим сезонную компоненту:

- для аддитивной модели – как разность между фактическими уровнями ряда y_t и центрированными скользящими средними;

- для мультипликативной модели – как частное от деления фактических уровней ряда на центрированные скользящие средние.

Используем эти оценки для расчета значений сезонной компоненты (таблица 2).

В моделях с сезонной компонентой предполагается, что сезонные воздействия за период взаимопогашаются. Это выражается в том, что сумма значений сезонной компоненты по всем кварталам равна: нулю для аддитивной модели и числу периодов в цикле для мультипликативной модели. Определяем корректирую-щий коэффициент k и скорректированные значения сезонной компоненты: 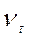= 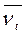- k или 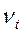= 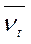k.

3. Исключим влияние сезонной компоненты: 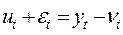или .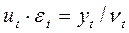

4. Определим составляющую 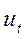. Для этого проведем аналитическое выравнивание ряда с помощью линейного тренда.

5. Определим 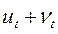или .

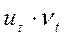6. Расчет ошибки производится по формулам соответственно: 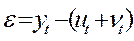или 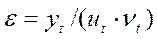. Для того, чтобы сравнить мультипликативную модель и другие модели, по аналогии с аддитивной моделью можно использовать сумму квадратов абсолютных ошибок .

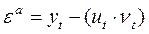Пример. Построим аддитивную модель по данным предыдущего примера. Таблица 1.

Номер квартала	Объем продаж	Скользящая средняя за 4 квартала	Центрированная скользящая средняя	Оценка сезонной вариации
			6,125	-1,125
		6,25	6,375	2,625
		6,5	6,625	0,375
		6,75	6,875	-1,875
			7,125	-1,125
		7,25	7,5	2,5
		7,75	7,75	0,25
		7,75	7,875	-0,875
			8,125	-2,125
		8,25	8,25	2,75
		8,25	8,125	0,875
			8,125	-1,125
		8,25	8,5	-3,5
		8,75

Заполним следующую таблицу.

Таблица 2.

	Номер квартала
			-1,125	2,625
	0,375	-1,875	-1,125	2,5
	0,25	-0,875	-2,125	2,75
	0,875	-1,125	-3,5		сумма
Среднее	0,5	-1,292	-2,25	2,75	-0,292
Скорректированная сезонная вариация	0,573	-1,219	-2,177	2,823

(корректирующий фактор k = -0,292/4)

Исключим сезонную вариацию.

Номер квартала	Объем продаж	Сезонная вариация, S	Десезонализированный объем продаж, Yt – S = T + E
		0,573	5,427083
		-1,219	5,21875
		-2,177	7,177083
		2,823	6,177083
		0,573	6,427083
		-1,219	6,21875
		-2,177	8,177083
		2,823	7,177083
		0,573	7,427083
		-1,219	8,21875
		-2,177	8,177083
		2,823	8,177083
		0,573	8,427083
		-1,219	8,21875
		-2,177	7,177083
		2,823	9,177083
		0,573	10,42708
		-1,219	10,21875

Уравнение линии тренда Т = 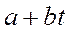. Найдем коэффициенты 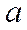и 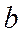по данным первого и последнего столбцов.

	ВЫВОД ИТОГОВ
	Регрессионная статистика
	Множественный R	0,878015
	R-квадрат	0,770911
	Нормированный R-квадрат	0,756593
	Стандартная ошибка	0,71808
	Наблюдения
	Дисперсионный анализ
		df	SS	MS	F	Значимость F
	Регрессия		27,76299	27,76299	53,84189	1,67E-06
	Остаток		8,250227	0,515639
	Итого		36,01321
		Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
	Y-пересечение	5,372889	0,353125	15,21527	6,17E-11	4,624299	6,12148
	t	0,239379	0,032623	7,337703	1,67E-06	0,170221	0,308537
	ВЫВОД ОСТАТКА
	Наблюдение	Предсказанное T	Остатки
		5,612269	-0,18519
		5,851648	-0,6329
		6,091027	1,086057
		6,330406	-0,15332
		6,569785	-0,1427
		6,809164	-0,59041
		7,048543	1,12854
		7,287922	-0,11084
		7,527301	-0,10022
		7,76668	0,45207
		8,006059	0,171024
		8,245438	-0,06836
		8,484818	-0,05773
		8,724197	-0,50545
		8,963576	-1,78649
		9,202955	-0,02587
		9,442334	0,984749
		9,681713	0,537037

Рассчитаем ошибки. MAD = 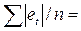0,484386.

MSE = 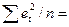0,458346.