Свойство 1. Дисперсия постоянной величины равна нулю: 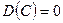 .
.
Доказательство. 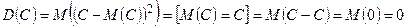 .
.
С другой стороны постоянная величина сохраняет одно и то же значение и рассеяния не имеет.
Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: 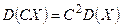 .
.
Доказательство. Используя определение дисперсии и свойства математического ожидания, имеем: 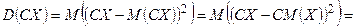
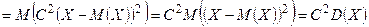 .
.
Свойство 3 Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих случайных величин: 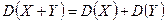 .
.
Доказательство. Используя терему 2 и свойства математического ожидания, 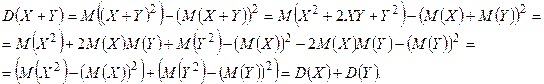
Следствие 1. Дисперсия суммы нескольких (конечного числа) независимых случайных величин равно сумме их дисперсий: 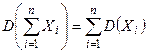 .
.
Следствие 2. 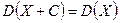 .
.
Следствие 3. Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих случайных величин: 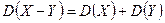 .
.
 2014-02-02
2014-02-02 4095
4095