Свойства функций автоковариации и автокорреляции

1. Максимум функций наблюдается при t= 0. Это очевидно, т.к. при t= 0 вычисляется степень связи отсчетов с собой же, которая не может быть меньше связи разных отсчетов. Значение максимума функции корреляции равно средней мощности сигнала.

2. Функции автокорреляции и автоковариации являются четными: R_X(t) = R_X(-t). Последнее также очевидно: X(t)X(t+t) = X(t-t)X(t) при t = t-t. Говоря иначе, моменты случайных величин X(t₁) и X(t₂) не зависят от последовательности, в которой эти величины рассматриваются, и соответственно симметричны относительно своих аргументов: R_x(t₁, t₂) = R_x(t₂, t₁), равно как и K_x(t₁, t₂) = K_x(t₂, t₁).

3. При tÞ ¥ значения ФАК для сигналов, конечных по энергии, стремятся к нулю, что прямо следует из физического смысла ФАК. Это позволяет ограничивать длину ФАК определенным максимальным значением t_max - радиусом корреляции, за пределами которого отсчеты можно считать независимыми. Интегральной характеристикой времени корреляции случайных величин обычно считают эффективный интервал корреляции, определяемый по формуле:

T_k =2 |r_x(t)| dt º (2/K_x(0)) |K_x(t)| dt. (13.7)

Отсчеты (сечения) случайных функций, отстоящие друг от друга на расстояние большее T_k, при инженерных расчетах считают некоррелированными.

Заметим, что для некоррелированных процессов при t Þ ¥ значение T_k стремится к 2, что несколько противоречит физическому смыслу радиуса корреляции, который в этом случае должен был бы стремиться к 1. С учетом последнего, эффективный интервал корреляции целесообразно определять по формуле:

T_k =2 |r_x(t)| d1 - t º (2/K_x(0)) |K_x(t)| d1 - t, (13.7')

либо вместо множителя 2 в (9.1.7) использовать множитель 1.

4. Если к случайной функции X(t) прибавить неслучайную функцию f(t), то ковариационная функция не изменяется.

Обозначим новую случайную функцию как Y(t)=X(t)+f(t). Функция математического ожидания новой величины: 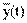= 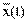+ f(t). Отсюда следует, что Y(t) - 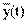= X(t) - 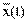, и соответственно K_y(t₁, t₂) = K_x(t₁, t₂).

5. Если случайную функцию X(t) умножить на неслучайную функцию f(t), то ее корреляционная функция R_x(t₁, t₂) умножится на f(t₁)×f(t₂). Обоснование данного свойства проводится по методике, аналогичной предыдущему пункту.

6. При умножении функции случайного процесса на постоянное значение С значения ФАК увеличиваются в С² раз.

Взаимные моменты случайных процессов второго порядка дают возможность оценить совместные свойства двух случайных процессов X(t) и Y(t) путем анализа произвольной пары выборочных функций x_k(t) и y_k(t).

Мера связи между двумя случайными процессами X(t) и Y(t) также устанавливается корреляционными функциями, а именно - функциями взаимной корреляции и взаимной ковариации. В общем случае, для произвольных фиксированных моментов времени t₁ = t и t₂ = t+t:

R_XY(t, t+t) = M{X(t) Y(t+t)}. (9.1.8)

K_XY(t, t+t) = M{(X(t)-m_x(t))(Y(t+t)-m_y(t+t))}. (13.9)

Взаимные функции являются произвольными функциями (не обладают свойствами четности или нечетности), и удовлетворяют следующим соотношениям:

R_xy(-t) = R_yx(t), (9.1.10)

|R_xy(t)|² £ R_x(0)R_y(0).

Если один из процессов центрированный, то имеет место R_xy(t) = K_xy(t).

Нормированная взаимная ковариационная функция (функция коэффициентов корреляции двух процессов), которая характеризует степень линейной зависимости между случайными процессами при сдвиге t одного процесса по отношению ко второму, определяется выражением:

r_xy(t) = K_xy(t)/(s_xs_y). (13.11)

Статистическая независимость случайных процессов определяет отсутствие связи между значениями двух случайных величин X и Y. Это означает, что плотность вероятности одной случайной величины не зависит от того, какие значения принимает вторая случайная величина. Двумерная плотность вероятностей при этом должна представлять собой произведения одномерных плотностей вероятностей этих двух величин:

p(x, y) = p(x) p(y).

Это условие является обязательным условием статистической независимости случайных величин. В противном случае между случайными величинами может существовать определенная статистическая связь. Как линейная, так и нелинейная. Мерой линейной статистической связи является коэффициент корреляции:

r_xy = [M{X·Y} – M{X}·M{Y}]/ 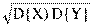= r_xy(0).

Значения r_xy могут изменяться в пределах от -1 до +1. В частном случае, если случайные величины связаны линейным соотношением x=ay+b, коэффициент корреляции равен ±1 в зависимости от знака константы а. Случайные величины некоррелированны при r_xy=0, при этом из выражения для r_xy следует:

M{X·Y} = M{X}·M{Y}.

Из статистической независимости величин следует их некоррелированность. Обратное не очевидно. Так, например, случайные величины x=cosj и y=sin j, где j - случайная величина с равномерным распределением в интервале 0…2p, имеют нулевой коэффициент корреляции, и вместе с тем их зависимость очевидна. Нулевой коэффициент корреляции в данном случае определяется взаимной ортогональностью функций cos j и sin j.

Классификация случайных процессов. Случайные процессы различают по степени однородности их протекания во времени (по аргументу).

Нестационарные процессы. В общем случае значения функций математического ожидания, дисперсии и корреляции могут быть зависимыми от момента времени t, т.е. изменяться во времени. Такие процессы составляют класс нестационарных процессов.

Стационарные процессы. Процесс называют стационарным, если плотность вероятностей процесса не зависит от начала отсчета времени, и если на интервале его существования выполняются условия постоянства математического ожидания и дисперсии, а корреляционная функция является функцией только разности аргументов t= t₂-t₁, т.e.:

m_x(t₁) = m_x(t₂) = m_x = 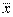= const, (13.12)

D_x(t₁) = D_x(t₂) = D_x = s² = const,

R_x(t₁, t₁+t) º R_x(t₂-t, t₂) = R_x(t) º R_x(-t),

r_x(t) = К_х(t)/D_x, r_x(0) = 1, |r_x(t)| ≤ 1, r_x(-t) = r_x(t).

Последние выражения свидетельствует о четности корреляционной (а равно и ковариационной) функции и функции корреляционных коэффициентов. Из него вытекает также еще одно свойство смешанных моментов стационарных процессов:

|R_x(t)| £ R_x(0), |K_x(t)| £ K_x(0) º D_x.

Чем медленнее по мере увеличения значений t убывают функции К_х(t) и r_x(t), тем больше эффективный интервал корреляции случайного процесса, и тем медленнее изменяются во времени его реализации.

Среди стационарных процессов выделяют строго стационарные процессы, для которых постоянны во времени не только математическое ожидание, дисперсия и корреляция, но и все остальные моменты высших порядков (в частности, асимметрия и эксцесс).

Стационарные случайные процессы наиболее часто встречаются при решении физических и технических задач. Теория стационарных случайных функций разработана наиболее полно и для ее использования обычно достаточно определения стационарности в широком смысле: случайная функция считается стационарной, если ее математическое ожидание постоянно, а корреляционная функция зависит только от одного аргумента. Случайные процессы, удовлетворяющие условиям стационарности на ограниченных, интересующих нас интервалах, также обычно относят к числу стационарных в широком смысле и называют квазистационарными.