Свойство 1 (правило повторного ожидания). Если 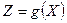 , где
, где 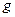 – некоторая неслучайная функция от Х, то
– некоторая неслучайная функция от Х, то 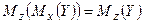 .
.
Следствие. 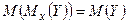 .
.
Доказательство проведём для непрерывной случайной величины. По определению имеем 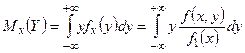 . Тогда
. Тогда
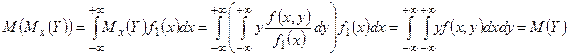 .
.
Свойство 2. Если 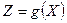 , где
, где 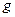 – некоторая неслучайная функция от Х, то
– некоторая неслучайная функция от Х, то 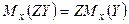 .
.
Свойство 3. Если случайные величины Х и У независимы, то 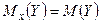 .
.
Пример 1. Дискретная двумерная случайная величина 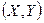 задана законом распределения:
задана законом распределения:
| У Х | 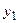 =3 =3 |  =6 =6 |
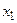 =1 =1 | 0,15 | 0,30 |
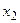 =3 =3 | 0,06 | 0,10 |
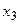 =4 =4 | 0,25 | 0,03 |
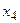 =8 =8 | 0,04 | 0,07 |
Найти условное математическое ожидание составляющей У при Х=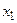 =1.
=1.
Решение. 1) Найдём 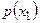 , для чего сложим вероятности, помещённые в строке
, для чего сложим вероятности, помещённые в строке 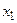 таблицы:
таблицы: 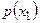 =0,15+0,30=0,45.
=0,15+0,30=0,45.
2) Найдём условное распределение вероятностей составляющей У при Х=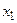 =1:
=1:
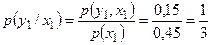 ,
, 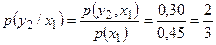 .
.
3) Найдём искомое условное математическое ожидание: 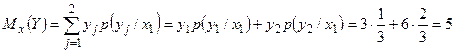 .
.
Ответ: 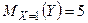 .
.
 2014-02-02
2014-02-02 1686
1686








