Числовые характеристики двумерных случайных величин

При изучении двумерных случайных величин рассматриваются числовые характеристики их одномерных составляющих Х и У – математические ожидания и дисперсии. Для их вычисления используются следующие формулы:

	Дискретная двумерная случайная величина	Непрерывная двумерная случайная величина
Математическое ожидание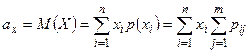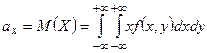
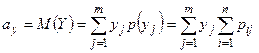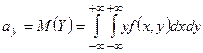Дисперсия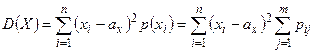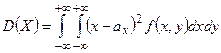

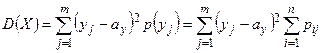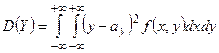Наряду с ними рассматриваются также числовые характеристики условных распределений: условные математические ожидания и условные дисперсии составляющих, которые могут быть определены формулами:

	Дискретная двумерная случайная величина	Непрерывная двумерная случайная величина
Математическое ожидание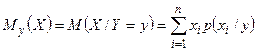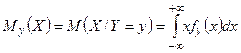
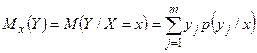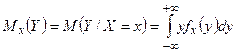Дисперсия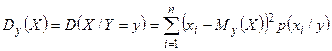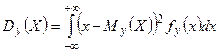

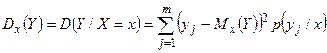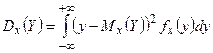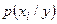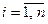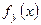В таблице () и – соответственно условные вероятности значений и условное распределение составляющей Х при условии, что ;

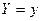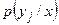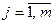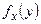() и – соответственно условные вероятности значений и условное распределение составляющей У при условии, что .

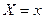Определение 1. Условное математическое ожидание 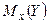случайной величины У при 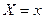называют функцией регрессии У по Х или регрессией У на Х.

Определение 2. Условное математическое ожидание 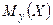случайной величины Х при 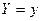называют функцией регрессии Х по У или регрессией Х на У.

Определение 3. Графики функций регрессии называют кривыми регрессии или линиями регрессии.