2014-02-03
788
Рис.72
Система имеет две степени свободы. Назначаем две обобщенные координаты s и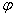 
.
Найдем обобщенную силу, соответствующую координате s. Даем приращение 
этой координате, оставляя координату 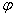неизменной, и вычислив работу единственной активной силы Р, получим обобщенную силу
.
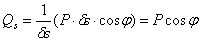Затем даем приращение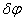 
координате 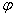, полагая s = const. При повороте стержня на угол 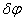точка приложения силы Р, колечко М, переместится на 
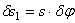. Обобщенная сила получится
.
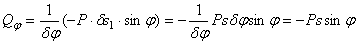Так как система консервативная, обобщенные силы можно найти и с помощью потенциальной энергии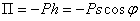 
. Получим 
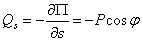и 
Получается гораздо проще.
По определению (7) обобщенные силы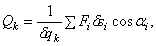 
k = 1,2,3,…, s, где s – число степеней свободы.
Если система находится в равновесии, то по принципу возможных перемещений (1)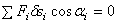 
. Здесь 
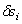– перемещения, допускаемые связями, возможные перемещения. Поэтому при равновесии материальной системы все ее обобщенные силы равны нулю:
Qk = 0, (k =1,2,3,…, s). (10)
Эти уравнения, уравнения равновесия в обобщенных координатах или уравнения равновесия Лагранжа, позволяют решать задачи статики еще одним методом.
|
|
|
Если система консервативная, то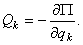 
Значит, в положении равновесия 
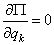. То есть в положении равновесия такой материальной системы ее потенциальная энергия либо максимальна, либо минимальна, т.е. функция 
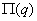имеет экстремум.
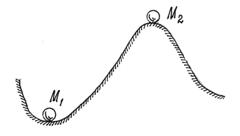
Это очевидно из анализа простейшего примера (рис.73). Потенциальная энергия шарика в положении М 1 имеет минимум, в положении М 2 – максимум. Можно заметить, что в положении М 1 равновесие будет устойчивым; в положении М 2 – неустойчивым.
