По определению (7) и (12) обобщенные силы
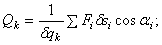
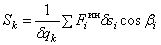 .
.
Сумма их 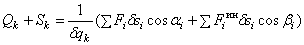 или
или
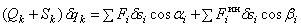 .
.
Но на основании общего уравнения динамика (3), правая часть равенства равна нулю. И так как все 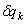 (k = 1,2,3,…, s) отличны от нуля, то
(k = 1,2,3,…, s) отличны от нуля, то 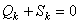 . Подставив значение обобщенной силы инерции (17), получим уравнение
. Подставив значение обобщенной силы инерции (17), получим уравнение
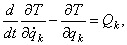 (k = 1,2,3,…, s). (18)
(k = 1,2,3,…, s). (18)
Эти уравнения называются дифференциальными уравнениями движения в обобщенных координатах, уравнениями Лагранжа второго рода или просто – уравнениями Лагранжа.
Количество этих уравнений равно числу степеней свободы материальной системы.
Если система консервативная и движется под действием сил потенциального поля, когда обобщенные силы 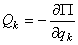 , уравнения Лагранжа можно составить по форме
, уравнения Лагранжа можно составить по форме
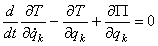 (19)
(19)
или 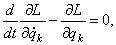 (k = 1,2,3,…, s), (20)
(k = 1,2,3,…, s), (20)
где L = T – П называется функцией Лагранжа (предполагается, что потенциальная энергия П не зависит от обобщенных скоростей).
Нередко при исследовании движения материальных систем оказывается, что некоторые обобщенные координаты qj не входят явно в функцию Лагранжа (или в Т и П). Такие координаты называют циклическими. Уравнения Лагранжа, соответствующие этим координатам, получаются проще.
Так как 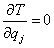 и
и 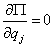 , то
, то 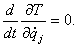
Первый интеграл таких уравнений находится сразу. Он называется циклическим интегралом:
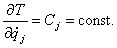 (21)
(21)
Дальнейшие исследования и преобразования уравнений Лагранжа составляют предмет специального раздела теоретической механики – «Аналитическая механика».
Уравнения Лагранжа обладают целым рядом достоинств в сравнении с другими способами исследования движения систем. Основные достоинства: методика составления уравнений одинакова во всех задачах, реакции идеальных связей не учитываются при решении задач.
И еще одно – эти уравнения можно использовать для исследования не только механических, но и других физических систем (электрических, электромагнитных, оптических и др.).
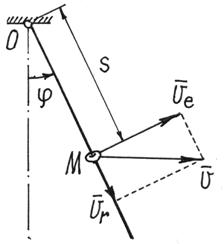
Пример 25. Продолжим исследование движение колечка М на качающемся стержне (пример 23).
Обобщенные координаты назначены – 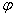 и
и 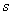 (рис.75). Обобщенные силы определены:
(рис.75). Обобщенные силы определены: 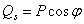 и
и 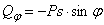 .
.
 2014-02-03
2014-02-03 2270
2270
