2014-02-03
1001
Рис.74
Рис.73
Равновесие считается устойчивым, если телу в этом положении сообщить малую скорость или сместить на малое расстояние и эти отклонения в дальнейшем не увеличатся.
Можно доказать (теорема Лагранжа-Дирихле), что если в положении равновесия консервативной системы ее потенциальная энергия имеет минимум, то это положение равновесия устойчиво.
Для консервативной системы с одной степенью свободы условие минимума потенциальной энергии, а значит и устойчивости положения равновесия, определяется, второй производной, ее значением в положении равновесия,
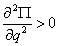. (11)
Пример 24. Стержень ОА весом Р может вращаться в вертикальной плоскости вокруг оси О (рис.74). Найдем и исследуем устойчивость положений равновесия.
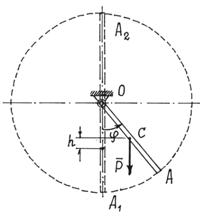
Стержень имеет одну степень свободы. Обобщенная координата – угол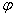 
.
Относительно нижнего, нулевого, положения потенциальная энергия П= Рh или
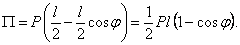
В положении равновесия должно быть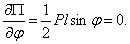 
Отсюда имеем два положения равновесия, соответствующие углам 
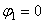и 
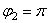(положения ОА 1 и ОА 2). Исследуем их устойчивость. Находим вторую производную 
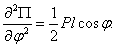Конечно, при 
, 
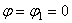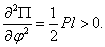Положение равновесия устойчиво. При 
, 
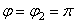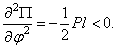Второе положение равновесия – неустойчиво. Результаты очевидны.
|
|
|
По той же методике (8), по которой вычислялись обобщенные силы Qk, соответствующие активным, задаваемым, силам, определяются и обобщенные силы Sk, соответствующие силам инерции точек системы:
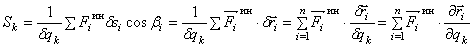(12)
И, так как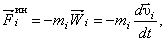 
то 
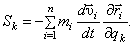(13)
Немного математических преобразований.
Очевидно,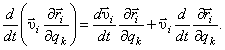 
Отсюда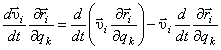 
. (14)
Так как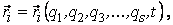 
а qk = qk(t), (k = 1,2,3,…, s), то
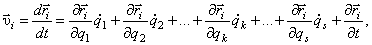где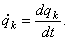 
Значит, частная производная скорости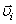 
по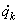 
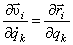. (15)
Кроме того, в последнем члене (14) можно поменять порядок дифференцирования:
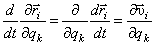. (16)
Подставляя (15) и (16) в (14), а потом (14) в (13), получим
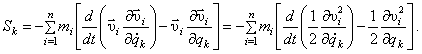
Разделив последнюю сумму на две и, имея ввиду, что сумма производных равна производной от суммы, получим
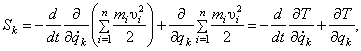(17)
где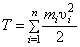 
– кинетическая энергия системы, 
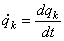- обобщенная скорость.
