Задача 4.
Задача 3.
Задача 2.
Задача 1.
Примеры решения типовых задач
Необходимо рассчитать сумму накопленного долга, если ссуда равна 10000 руб., срок долга – 4 года при ставке простого процента, равной 10% годовых.
Решение:
Используем формулу (5).
F = 10000 (1+0.1*4) = 14000 руб.
Определить, какую сумму (P) получит должник и сумму дисконта (D), если через 180 дней с момента подписания контракта должник уплатит 50000 руб., кредит предоставлен под 15% годовых по схеме простых процентов и при условии, что временная база равна 365 дням.
Решение:
Используем формулу (7).
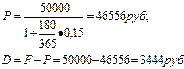
В какую сумму обратится долг, равный 10000 руб., через 5 лет и 52 года при росте по сложной ставке 9%?
Решение:
По таблице 1 сложных процентов (смотри приложение 1) находим величину финансового множителя FM1 и сумму долга через 5 лет.
FM1=1,0555=1,30696, откуда F=10000 1,306956 = 13069,6 руб.
Срок ссуды n=52 года. В этом случае находим два табличных значения множителя FM1: 1,05550 и 1,0552.
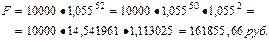
Необходимо определить настоящую (текущую) величину 50000 руб., которые будут выплачены через 1) 5 лет и 2) 52 года по сложной ставке процентов, равной 5%.
Решение:
Используем формулу (8).
Величину дисконтного множителя (FM2) находим по таблице 2 приложения: 1,05-5=0,78353. Откуда
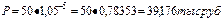
Если на эту сумму наращивать сложные проценты (5%), то к концу 5-летия она увеличится до 50000 руб.
Срок ссуды равен 52 годам:
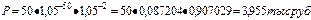
Если на эту сумму наращивать сложные проценты (5%), то к концу 52 года она увеличится до 50000 руб.
Тема 3. Методы оценки эффективности
инвестиционных проектов
 2014-02-03
2014-02-03 994
994








