Диверсификация позволяет устранить несистематический (диверсифицируемый) риск портфеля акций. Систематический риск, обусловленный факторами глобального характера, с помощью диверсификации устранить или снизить нельзя. Для устранения систематического риска используется процедура хеджирования, связанная с включением в портфель акций фьючерсов или опционов. Возможность использования производных финансовых инструментов вытекает из индексной модели Шарпа для оценки эффективности ценной бумаги:
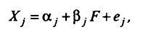
где Xj - ожидаемая доходность (эффективность) портфеля;
α j - доходность портфеля при условии отсутствия воздействия рыночных факторов;
βj - бета-коэффициент портфеля;
F ~ ожидаемая доходность рыночного портфеля, представленная фондовым рыночным индексом;
еj - ошибка, являющаяся независимой случайной переменной с постоянной дисперсией и нулевым математическим ожиданием, ее ковариации с остальными случайными переменными, входящими в уравнение, равны нулю.
В целом для портфеля акций можно записать:
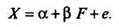
Бета-коэффициент характеризует рыночный (систематический, не диверсифицируемый) риск портфеля, для устранения которого и могут использоваться фьючерсные и опционные контракты на фондовый индекс. Это могут быть, например, реальные контракты на индекс Российской торговой системы или внебиржевые форвардные контракты на расчетный индекс. Для изучения хеджирования портфеля акций рассмотрим модельный фондовый индекс 1п, рассчитанный по курсам акций L эмитентов для n -го момента времени:
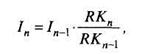
где In - текущее значение индекса;
In-1 - значение индекса на предыдущих торгах (примем I0 = 100);
RKn и RKn -1 - суммарная рыночная капитализация акций L эмитентов, входящих в расчет индекса, по п-м и (n -1)-м торгам.
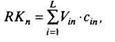
где Vin - общее количество акций i -го эмитента, находящихся в обращении во время
n -й торговой сессии;
сin - средневзвешенная цена акций 1-го эмитента по результатам торгов n -й торговой сессии.
Сформируем фьючерсный (или форвардный) контракт на этот индекс. Базовым активом такого контракта является индекс Iп условного рыночного портфеля акций L эмитентов. Контракт носит расчетный характер, реальная поставка базового актива при исполнении контракта не производится. Ценой закрытия контракта в день t служит значение индекса It. Цена контракта измеряется в индексных пунктах или в денежных единицах. Во втором случае вводится денежная стоимость одного индексного пункта.
Предположим, что инвестор имеет портфель акций L эмитентов, по структуре аналогичный рыночному портфелю. Суммарную стоимость портфеля будем измерять в индексных пунктах. Если портфель куплен по цене 10 (при значении индекса, равном I0), то его стоимость в зависимости от изменений рыночного индекса графически будет иметь вид наклонной линии (рис. 12.2, линия "Акции"). При снижении в будущем значений индекса In менее 10 стоимость портфеля будет уменьшаться, а при увеличении 1п более I0 стоимость портфеля будет возрастать.
Возможность снижения стоимости портфеля обусловлена систематическим риском, который воздействует на рынок в целом. Для снижения систематического риска портфеля нужно включить в него соответствующее число коротких фьючерсов или форвардов на индекс In.
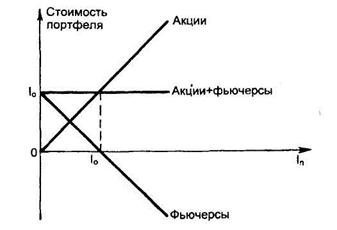
Рис. 12.2. Зависимость стоимости портфеля акций и короткого
индексного фьючерса на рыночный индекс
Пусть портфель акций дополняется коротким индексным фьючерсом, открытым по фьючерсной цене, соответствующей значению индекса I0. Зависимость дохода по фьючерсу от значения рыночного индекса показана на рис. 12.2 (линия "Фьючерс"). Тогда суммарная стоимость портфеля с фьючерсом (рис. 12.2, линия "Акции + фьючерс") становится постоянной и не зависит от изменений фондового индекса.
Более предпочтительных для инвестора результатов можно добиться, включив в портфель вместо короткого индексного фьючерса длинный пут опцион на индексный фьючерс со страйком (I0 + П), где П - опционная премия. Результат такого хеджирования приведен на рис. 12.3.

Рис. 12.3. Зависимость стоимости портфеля акций с длинным
пут опционом на фьючерс на рыночный индекс
Использование длинного пут опциона делает стоимость суммарного портфеля акций и опциона постоянной на интервале рыночного индекса, где ожидается падение стоимости портфеля без опциона, а на интервале, где ожидается рост стоимости портфеля акций без опциона, добавление опциона в портфель не ликвидирует этот рост (рис. 12.3, линия "Акции + опцион").
Хеджирование портфеля акции фьючерсом и пут опционом на индекс рассматривалось на примере рыночного портфеля. Но реальные портфели акций инвесторов крайне редко по своей структуре совпадают с рыночным портфелем, поэтому не для каждого портфеля при хеджировании может быть использован фьючерсный или опционный контракт на рыночный индекс. Возможность использования срочного контракта на фондовый индекс для хеджирования портфеля определяется по величине коэффициента корреляции между портфельным и рыночным индексами. Когда значение такого коэффициента корреляции по абсолютной величине больше 0,6, то хеджирование данного портфеля срочными контрактами на рыночный индекс возможно, в противном случае - нет. Если же коэффициент корреляции отрицателен и по абсолютной величине больше 0,6, то для хеджирования нужно открывать либо длинную позицию по фьючерсу, либо длинную позицию по колл опциону на индексный фьючерс. Для хеджирования портфеля акций не обязательно использовать срочные контракты на рыночный индекс. Здесь могут быть использованы срочные контракты на любой другой актив (валюта, процентные ставки, фондовый индекс другого рынка, индекс доходности государственных облигаций, товары и т.д.). Необходимо только чтобы выполнялось условие высокой корреляции рыночной стоимости этого актива с индексом портфеля.
Учитывая эти обстоятельства, можно уточнить понятия хеджирования и диверсификации. Хеджирование инвестиционного портфеля акций - процесс снижения риска портфеля путем включения в него срочного контракта на высококоррелированный с портфелем актив. Диверсификация инвестиционного портфеля акций - процесс снижения риска портфеля путем включения в него слабокоррелированных друг с другом акций.
 2014-02-02
2014-02-02 2112
2112








