Геометрический смысл производной

Возьмем на непрерывной кривой L две точки М и М ₁(см. рис. 2).

Прямую MM ₁, проходящую через эти точки, называют секущей.

Пусть точка М ₁, двигаясь вдоль кривой L, неограниченно приближа­ется к точке М. Тогда секущая, поворачиваясь около точки М, стремится к некоторому предельному положению МТ.

Касательной к данной кривой в данной точке М называется предельное положение МТ секущей MM ₁, проходящей через точку М, ко­гда вторая точка пересечения М ₁ неограниченно приближается по кривой к точке М.

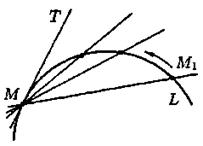
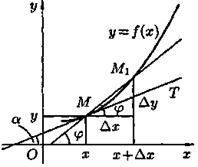
Рис. 2. Рис. 3.

Рассмотрим график непрерывной кривой у = f (x), имеющий в точке

М (x; у)невертикальную касательную. Найдем ее угловой коэффи­циент k= tg α,где α — угол касательной с осью Ох.

Для этого проведем через точку М и точку М ₁графика с абсциссой х + ∆x; секущую (см. рис. 3). Обозначим через φ — угол между секущей МM ₁ и осью Ох. На рисунке видно, что угловой коэффициент секущей

k _сек.=tg φ ==.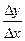

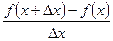При ∆x → 0 в силу непрерывности функции приращение ∆у тоже стре­мится к нулю; поэтому точка M ₁ неограниченно приближается по кривой к точке М, а секущая ММ ₁, поворачиваясь около точки М, переходит в касательную. Угол φ → α, т. е. .

Следовательно,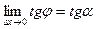

Поэтому угловой коэффициент касательной равен

k = tg α = 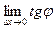= =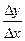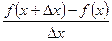. (7.5)

Следовательно, угловой коэффициент касательной 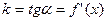, то есть производная 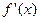в точке 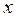равна угловому коэффициенту касательной к графику функции 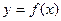в точке, абсцисса которой равна 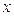. В этом заключается геометрический смысл производной.

Если точка касания 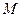имеет координаты 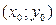(рис.4), то угловой коэффициент касательной есть 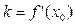. Пользуясь уравнением прямой, проходящей через заданную точку в заданном направлении 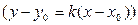, можно записать уравнения касательной: .

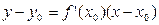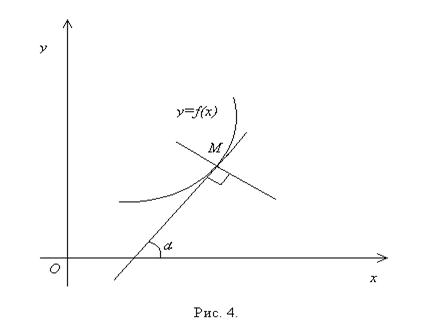
Прямая, перпендикулярная касательной в точке касания, называется нормалью к кривой.

Так как нормаль перпендикулярна касательной, то ее угловой коэффициент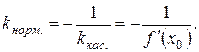

Поэтому уравнение нормали имеет вид 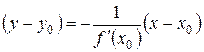(если ).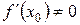

Теорема. Если функция дифференцируема в некоторой точке, то она непрерывна в ней.