Пусть у = f (и) и и = φ (x), тогда у=f (φ (x)) — сложная функция с промежуточным аргументом и и независимым аргументом х.
Теорема. Если функция и = φ (х)имеет производную 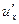 в точке х, а функция у = f (u)имеет производную
в точке х, а функция у = f (u)имеет производную 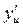 в соответствующей точке и = φ(х), то сложная функция у = f (φ(x))имеет производную
в соответствующей точке и = φ(х), то сложная функция у = f (φ(x))имеет производную 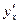 в точке х,которая находится по формуле
в точке х,которая находится по формуле 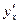 =
= 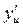 ·
·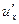 .
.
6. 8. Производная обратной функции
Пусть функция 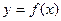 определена, монотонно возрастает (убывает) и непрерывна в некотором промежутке
определена, монотонно возрастает (убывает) и непрерывна в некотором промежутке 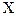 . Тогда в соответствующем промежутке
. Тогда в соответствующем промежутке 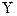 значений этой функции существует однозначная обратная функция
значений этой функции существует однозначная обратная функция 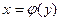 , так же монотонно возрастающая (убывающая) и непрерывная.
, так же монотонно возрастающая (убывающая) и непрерывная.
Теорема. Если функция у = f (x) строго монотонна на интервале (a; b) и имеет неравную нулю производную f ′(x) в произвольной точке этого интервала, то обратная ей функция x = φ(у)также имеет производную φ'(у)в соответствующей точке, определяемую равенством 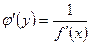 или
или 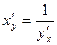 .
.
Правило дифференцирования обратной функции записывают так:
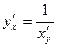 или
или 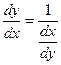
 2014-02-03
2014-02-03 2186
2186
