Методом математической индукции можно показать, что
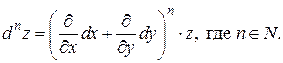
Отметим, что полученные формулы справедливы лишь в том случае, когда переменные х и у функции 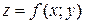 являются независимыми.
являются независимыми.
Пусть 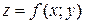 – функция двух переменных
– функция двух переменных 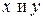 , каждая из которых является функцией независимой переменной t:
, каждая из которых является функцией независимой переменной t:  В этом случае функция
В этом случае функция 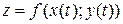 является сложной функцией одной независимой переменной t; переменные
является сложной функцией одной независимой переменной t; переменные 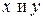 – промежуточные переменные.
– промежуточные переменные.
Теорема 3. Если 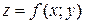 – дифференцируемая в точке
– дифференцируемая в точке  функция и
функция и 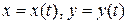 – дифференцируемые функции независимой переменной t, то производная сложной функции
– дифференцируемые функции независимой переменной t, то производная сложной функции 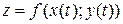 вычисляется по формуле
вычисляется по формуле
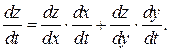 (8)
(8)
Дадим независимой переменной t приращение 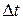 . Тогда функции
. Тогда функции 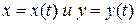 получат приращения
получат приращения 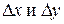 соответственно. Они, в свою очередь, вызовут приращение
соответственно. Они, в свою очередь, вызовут приращение 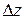 функции z. Так как по условию функция
функции z. Так как по условию функция 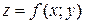 дифференцируема в точке
дифференцируема в точке  , то её полное приращение можно представить в виде
, то её полное приращение можно представить в виде
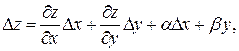
где 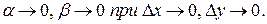 Разделим выражение
Разделим выражение 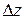 на
на 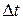 и перейдем к пределу при
и перейдем к пределу при 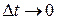 . Тогда
. Тогда 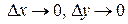 в силу непрерывности функций
в силу непрерывности функций 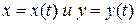 (по условию теоремы они дифференцируемы). Получаем:
(по условию теоремы они дифференцируемы). Получаем:
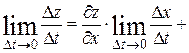
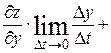
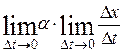
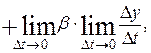
т. е.
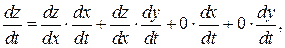
или
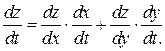
Частный случай: 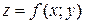 , где
, где 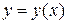 , т. е.
, т. е. 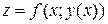 – сложная функция одной независимой переменной х. Этот случай сводится к предыдущему, причем роль переменной t играет х. Согласно формуле (8) имеем:
– сложная функция одной независимой переменной х. Этот случай сводится к предыдущему, причем роль переменной t играет х. Согласно формуле (8) имеем:
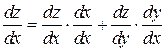 или
или 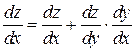 (9)
(9)
Формула (9) носит название формулы полной производной.
Общий случай: 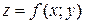 , где
, где 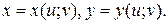 Тогда
Тогда 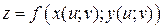 – сложная функция независимых переменных
– сложная функция независимых переменных 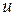 и
и 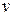 . Её частные производные
. Её частные производные 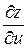 и
и 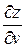 можно найти, используя формулу (8) следующим образом. Зафиксировав
можно найти, используя формулу (8) следующим образом. Зафиксировав 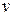 , заменяем в ней
, заменяем в ней 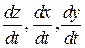 соответствующими частными производными
соответствующими частными производными 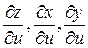 :
:
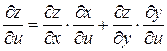 (10)
(10)
Аналогично получаем: 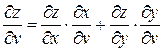 .
.
Таким образом, производная сложной функции 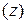 по каждой независимой переменной
по каждой независимой переменной 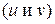 равна сумме произведений частных производных этой функции
равна сумме произведений частных производных этой функции 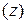 по её промежуточным переменным
по её промежуточным переменным 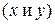 на их производные по соответствующей независимой переменной
на их производные по соответствующей независимой переменной 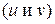 .
.
Используя правило дифференцирования сложной функции, можно показать, что полный дифференциал обладает свойством инвариантности: полный дифференциал функции 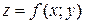 сохраняет один и тот же вид независимо от того, являются ли аргументы независимыми переменными или функциями независимых переменных.
сохраняет один и тот же вид независимо от того, являются ли аргументы независимыми переменными или функциями независимых переменных.
Пусть 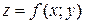 , где x и y – независимые переменные. Тогда полный дифференциал (1-го порядка) функции имеет вид
, где x и y – независимые переменные. Тогда полный дифференциал (1-го порядка) функции имеет вид
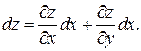
Рассмотрим сложную функцию 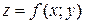 , где
, где 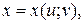
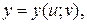 т. е. функцию
т. е. функцию 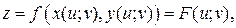 где
где 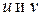 – независимые переменные.
– независимые переменные.
Тогда имеем:
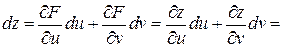
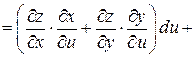
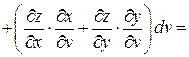
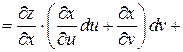
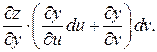
Выражения в скобках представляют собой полные дифференциалы dx и dy функций 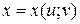 и
и 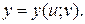 Следовательно, и в этом случае,
Следовательно, и в этом случае,
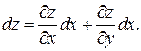
 2014-02-02
2014-02-02 775
775








