Правила дифференцирования

Таблица производных

Формулы дифференцирования

1. (с)' = 0;

2. (u ^α)' = α · u ^{α -1} · u ', в частности, ;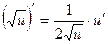

3. , в частности,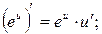

4. 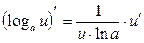в частности, ;

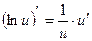5. (sin u)' = cos u · u ′; 6. (cos u)' = - sin u · u ′;

7. (tg u)' = 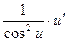; 8. (ctg u)' = ;

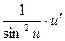9. (arcsin u)' = 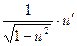; 10. (arccos u)' = -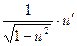

11. (arctg u)' = 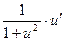; 12. (arcctg u)' = - ;

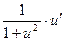13. (sh u)' = ch u · u '; 14. (ch u)' = sh u · u ';

15. (th u)' = 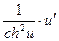; 16. (cth u)' = -.

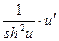Выведенные правила дифференцирования, формулы производных основных элементарных функций запишем в виде таблицы.

На практике чаще всего приходится находить производные от сложных функций. Поэтому в приведенной ниже таблице формул дифференцирования аргумент «x» заменен на промежуточный аргумент «u».

1. (u ± v)' = u ' ± v ';

2. (u · v)' = u ' v + uv ′, в частности, (cu)′ = с · u ';

3. 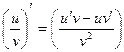, в частности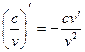

4. 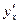= 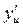· 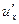, если y = f (u), u = φ (x);

5. 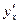= 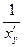, если у = f (x) и x = φ (y);