2014-02-03
220
Расчёт реакции системы на типовое воздействие в установившемся режиме
1. 
.
Необходимо найти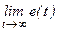 
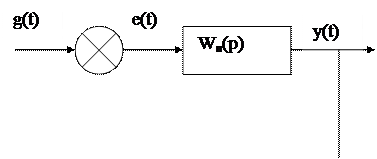
e(t)=g(t)-y(t)=g(t)-Wn(р)*e(t)
.
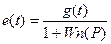
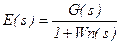Так как изображение по Лапласу единичной ступенчатой функции равно
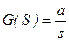, то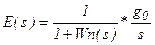 
.
Если 
, то
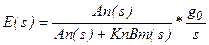
Как известно, по правилу предельного перехода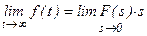 
, тогда
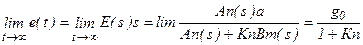
Чем больше Кп, тем меньше величина установившейся ошибки, но она не будет равна 0 и она называется статической. Для того чтобы установившаяся ошибка была равна нулю, нужно чтобы в числителе последнего выражения был множитель s или знаменатель передаточной функции прямой цепи имел множителем s в какой либо степени, не равной нулю: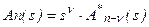 
.
В этом случае установившаяся ошибка
.
Такая система называется астатической с порядком астатизма ν. Для того, что бы система была астатической надо, чтобы прямая цепь содержала ν интегрирующих звеньев.
| Коэффициент |
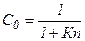называют коэффициентом статической ошибки.
2. Входное воздействие линейно зависит от t: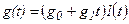 
Тогда:
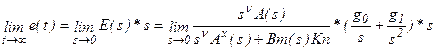
Если 
, то ошибка стремится к бесконечности.
Если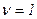 
, то ошибка равна 
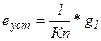, а коэффициент скоростной ошибки равен 
.
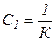Если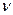 
=2, то 
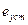=0.
Если записать Е(s)=Wge(s)*G(s) и разложить Wge(s) в ряд Тейлора по переменной s в окрестности 0
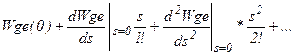, то
....
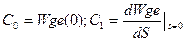Для того, что бы уменьшить установившуюся ошибку – необходимо увеличить порядок астатизма системы, но стоит учитывать что это ведет к ухудшению устойчивости.
