Математические модели объектов и САУ
Для формализованного описания САУ используют три вида моделей (все они математические):
- Модели представления системы во временной области – модели в пространстве состояний;
- Модели представления системы в частотной области, получившие название вход/выход, получившие название операторная модель;
- Структурные схемы – графические модели.
Для исследования процессов САУ необходимо в любом виде моделей составить описание ее в виде системы дифференциальных уравнений. Необходимо установить значение всех начальных условий, определить вид функций, описывающих внешнее воздействие.
Математическая модель САУ в терминах преобразования «вход/выход»
В инженерной практике большое распространение получил операторный метод исследования системы, который использует некоторые специальные функции, характерные динамические свойства САУ, такие как передаточная функция, переходные функции и различные частотные функции.
Для этого метода справедливо:
- Каждый реальный элемент САУ – это устройство, звено системы, в котором осуществляется образование одного воздействия (входного процесса) в другое (выходная реакция или выходной процесс);
- Взаимодействие между звеньями создаются путем описания связей между их входами и выходами, определяющими структуру САУ.
Пусть нам задано, что рассматриваемая линейная функция САУ, для описания которой используется линейное дифференциальное уравнение, записываемое в следующем виде:
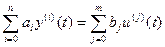 ;
; 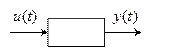
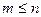 ;
;
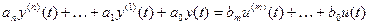 , где
, где
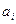 и
и 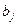 – параметры системы.
– параметры системы.
Возьмем оператор дифференцирования для представления системы в операторной форме:
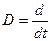 – оператор дифференцирования;
– оператор дифференцирования;
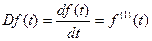 ;
;
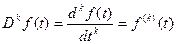 .
.
Перепишем используя оператор дифференцирования:
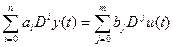 ;
;
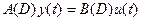 , где ‚
, где ‚
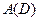 и
и 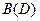 – многочлены
– многочлены 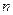 -ой степени
-ой степени
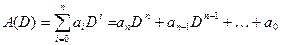 ;
;
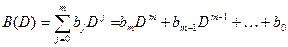 .
.
Разделим левую и правую части операторной формы на 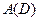 :
:
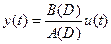 ; ƒ
; ƒ
Вводится операторная передаточная функция:
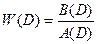 ;
;
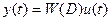 .
.
Представление системы в виде ƒ является символическим, оно не даст решения дифференциального уравнения, т.к. не определен смысл деления на 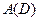 .
.
 2014-02-02
2014-02-02 743
743








