Несколько интерпретаций теоремы Ляпунова

1. Если невозмущенное движение устойчиво, то при достаточно малых начальных возмущениях возмущенное движение будет сколь угодно мало отличаться от невозмущенного движения;
2. Если невозмущенное движение не устойчиво, то возмущенное движение будет отходить от него, как бы малы не были начальные возмущения;
3. Если невозмущенное движение устойчиво и при этом любое возмущенное движение при малых начальных возмущениях стремиться к невозмущенному движению, при этом норма вектора будет стремиться к 0, то невозмущенное движение называется асимптотически устойчивым

.

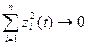Линейная стационарная система асимптотически устойчива тогда и только тогда, если корни характеристического уравнения 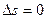имеют отрицательные вещественные части.

Пусть 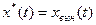, тогда возмущенным движением будет реальная траектория системы.

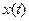- возмущение.

;

;

;

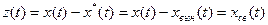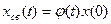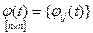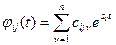; – определяется корнями характеристического уравнения

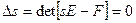– определяется только матрицей динамики

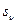– корни характеристического уравнения.

;

,

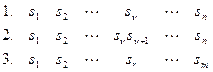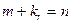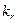– кратный корень 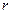-ой кратности.

1. Пусть корни характеристического уравнения простые и вещественные
   
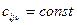
   Если корни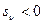 , то

1. ,

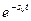
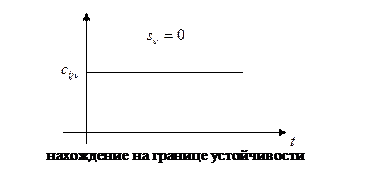
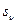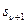
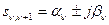
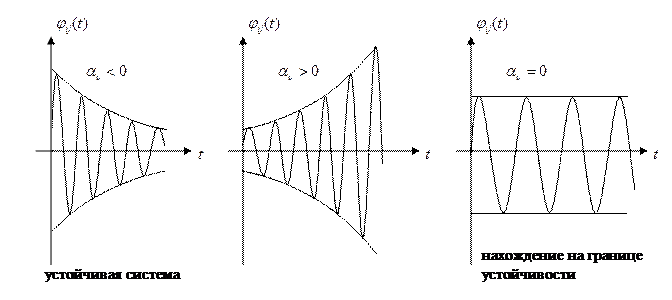
¬ – устойчивая система второго порядка (вещественная часть отрицательная);

n – неустойчивая система третьего порядка;

«– апериодическая устойчивость;

t – колебательная устойчивость;

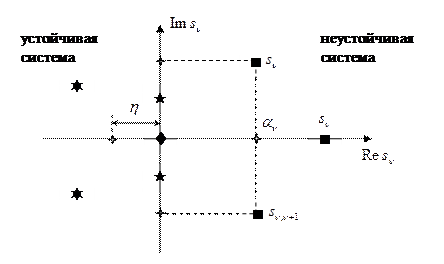
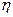– запас устойчивости для устойчивой системы.