Линейная система является устойчивой по Ляпунову, если все характеристические числа динамики матрицы 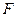 имеют отрицательные или нулевые вещественные части, причем в последнем случае характеристические числа должны быть простые. При нарушении хотя бы одного из условий система не устойчива.
имеют отрицательные или нулевые вещественные части, причем в последнем случае характеристические числа должны быть простые. При нарушении хотя бы одного из условий система не устойчива.
Линейная система асимптотически устойчива тогда и только тогда, когда все характеристические числа матрицы 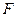 имеют отрицательные вещественные части.
имеют отрицательные вещественные части.
Примечание: если в характеристическом уравнении имеется хотя бы один нулевой корень 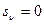 или хотя бы одна пара чисто мнимых корней
или хотя бы одна пара чисто мнимых корней 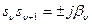 , а все остальные корни имеют отрицательные вещественные части, то говорят, что система находится на границе устойчивости. В первом случае граница апериодической устойчивости, во втором – граница колебательной устойчивости.
, а все остальные корни имеют отрицательные вещественные части, то говорят, что система находится на границе устойчивости. В первом случае граница апериодической устойчивости, во втором – граница колебательной устойчивости.
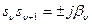
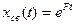 – асимптотически устойчивая система
– асимптотически устойчивая система
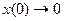 .
.
 2014-02-02
2014-02-02 490
490








