Критерий Михайлова. Задано характеристическое уравнение

Пример

Пример

Задано характеристическое уравнение:

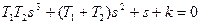
Определить значения параметров 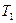, 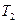и 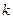при которых система устойчива.

Решение:

;

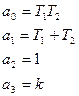
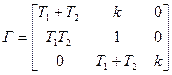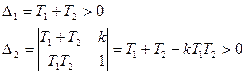
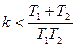
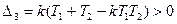
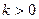
Область устойчивости для параметра :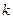

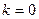– нижняя граница;

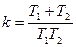– верхняя граница.

Задана матрица :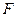

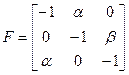
Определить устойчивость.

Решение:

;

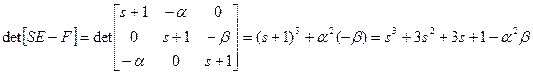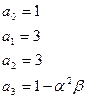
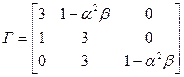
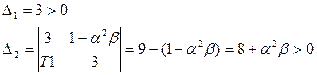
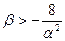
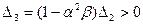
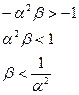
Область устойчивости:

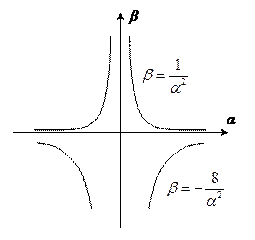
Основой для критерия является комплексная частотная характеристика.

;

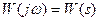
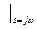
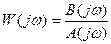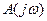– связано с устойчивостью (т.к. это характеристический многочлен).

Для построения годографа меняют значения 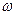от 0 до .

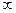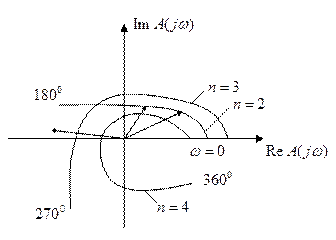
Для устойчивости линейной системы по отклонению начальных условий с частотной характеристикой 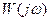необходимо и достаточно, чтобы годограф характеристического многочлена 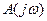при изменении частоты от 0 до 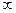, охватывал начало координат на угол

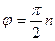, где

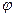– угол;

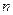– порядок характеристического многочлена.

Алгоритм:

1. Определить порядок 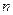знаменателя 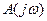комплексно-частотной характеристики ;
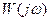2. Построить на комплексной плоскости годограф , ;
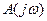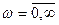3. Рассчитать величину 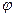угла на которой годограф охватывает начало координат , ;
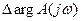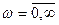4. Проверить выполнение условий. Если приращение равно 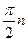, то система устойчива.