Критерий Гурвица. Для определения устойчивости систем высокого порядка выделяют правила, которые позволяют определить устойчивость системы без вычисления корней

Критерии устойчивости

Для определения устойчивости систем высокого порядка 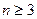выделяют правила, которые позволяют определить устойчивость системы без вычисления корней характеристического уравнения. Эти правила называются критериями устойчивости. Они бывают:

• Алгебраические:

• критерий Рауса;
• критерий Гурвица;
• критерий Льенара

• Частотные:

• критерий Михайлова;
• критерий Найквиста.

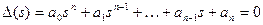
Матрица Гурвица:

.

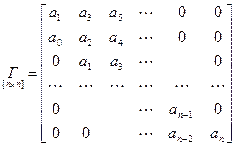На главной диагонали в порядке возрастания располагаются коэффициенты 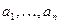. Каждый из столбцов заполняется вверх с возрастающими индексами, вниз – с убывающими индексами.

Определение устойчивости по Гурвицу: для устойчивости линейной системы необходимо и достаточно чтобы были положительны 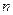главных определителей матрицы Гурвица.

Главные определители имеют вид:

;

;

;

.

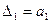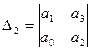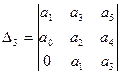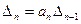Гурвиц показал, что:

• если 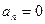, то система находится на границе апериодической устойчивости;
• если 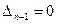, то система находится на границе колебательной устойчивости, т.е. есть пара мнимых корней.