Введем понятие типовой импульсной цепи, в которую входит идеальный импульсный элемент («ключ») и непрерывная часть с передаточной функцией 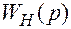 (рис. 2.1). Рассмотрим динамику этой цепи, ее входной и выходной сигналы только в дискретные моменты времени
(рис. 2.1). Рассмотрим динамику этой цепи, ее входной и выходной сигналы только в дискретные моменты времени 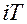 (для чего на выходе цепи показан фиктивный квантователь, работающий синхронно с входным квантователем). Тогда передаточные свойства импульсной цепи можно характеризовать с помощью дискретной передаточной функции (д.п.ф.)
(для чего на выходе цепи показан фиктивный квантователь, работающий синхронно с входным квантователем). Тогда передаточные свойства импульсной цепи можно характеризовать с помощью дискретной передаточной функции (д.п.ф.)
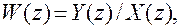 (2.6)
(2.6)
где 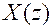 и
и 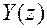 — z -изображение входного и выходного сигналов цепи.
— z -изображение входного и выходного сигналов цепи.
Д.п.ф. 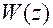 импульсной цепи связана с весовой функцией
импульсной цепи связана с весовой функцией 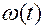 непрерывной части z -преобразованием:
непрерывной части z -преобразованием:
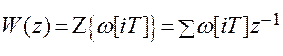 . (2.7)
. (2.7)
Непрерывная часть цепи задана обычно в виде передаточной функции 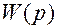 , поэтому для отыскания функции
, поэтому для отыскания функции 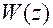 необходимо предварительно находить весовую функцию
необходимо предварительно находить весовую функцию 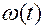 .
.
Так как в таблицах соответствия изображения по Лапласу и 2-изображения обычно указываются рядом, то функцию 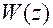 можно определить сразу по виду функции
можно определить сразу по виду функции 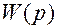 . Этому непосредственному переходу от
. Этому непосредственному переходу от 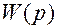 к
к 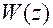 соответствует условная запись
соответствует условная запись
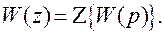 (2.8)
(2.8)
Если в типовой цепи после «ключа» стоит фиксатор, то д.п.ф. всей цепи может быть определена по формуле:
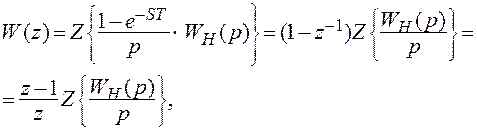 (2.9)
(2.9)
где 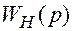 — передаточная функция непрерывной части (не включающей фиксатор).
— передаточная функция непрерывной части (не включающей фиксатор).
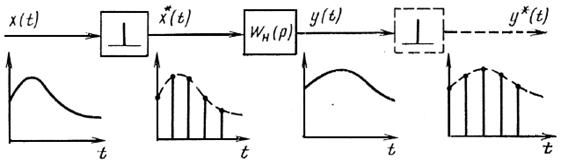
Рис. 2.1 Типичный участок импульсной системы
Пример. Найдем д.п.ф. цепи, состоящей из “ключа” и инерционного звена первого порядка (без фиксатора на его входе)
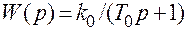 .
.
Весовая функция звена
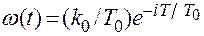
или
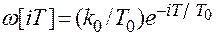
Согласно таблице 2.1 д.п.ф. цепи:
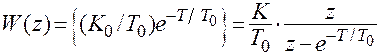
Изложенные приемы математического описания импульсных систем с помощью z -изображений и соответствующих им разностных уравнений удобно использовать для цифрового моделирования чисто непрерывных систем на ЭВМ. Но если для цифрового моделирования используются точные д.п.ф. полученные по формуле (2.7) или по таблицам соответствия, то необходимо предварительно, перед переходом к разностному уравнению, найти д.п.ф. 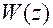 , устанавливающую связь между огибающими входной и выходной дискретных последовательностей:
, устанавливающую связь между огибающими входной и выходной дискретных последовательностей:
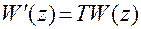 .
.
Множителем Т компенсируется ослабление сигналов, которое вносится реально квантователем в импульсной системе (и которое отсутствует в моделируемой непрерывной системе!).
Любую д.п.ф., 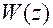 или
или 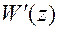 , в общем случае можно представить в виде отношения полиномов переменной z:
, в общем случае можно представить в виде отношения полиномов переменной z:
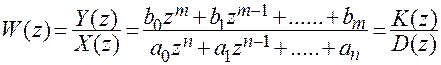 (2.10)
(2.10)
или
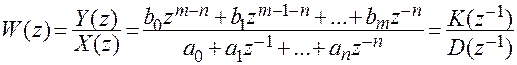 (2.11)
(2.11)
Передаточной функции (2.11) соответствует операторное уравнение динамики импульсной цепи в z-форме:
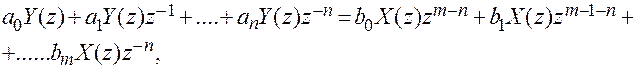 по которому легко получить разностное уравнение импульсной цепи или моделируемой непрерывной системы:
по которому легко получить разностное уравнение импульсной цепи или моделируемой непрерывной системы:
 (2.12)
(2.12)
Разностные уравнения вида (2.12) обладают важным преимуществом перед обыкновенными дифференциальными уравнениями: разрешенные относительно 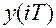 они уже в самой своей записи содержат алгоритм решения, который легко программируется на ЦВМ. Кроме того, разностные уравнения можно также представлять в виде сигнальных диаграмм состояния, удобных для моделирования. Основным операционным элементом дискретной диаграммы состояния вместо аналогового интегратора является элемент задержки
они уже в самой своей записи содержат алгоритм решения, который легко программируется на ЦВМ. Кроме того, разностные уравнения можно также представлять в виде сигнальных диаграмм состояния, удобных для моделирования. Основным операционным элементом дискретной диаграммы состояния вместо аналогового интегратора является элемент задержки 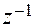 .
.
Пример. Определим точную д.п.ф. импульсной цепи, состоящей из “ключа”, фиксатора и идеального интегратора:
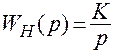 .
.
Согласно (2.9) и таблице 2.1 точная д.п.ф.:
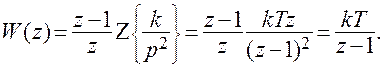 (2.13)
(2.13)
 2014-02-02
2014-02-02 543
543








