Свойства определенного интеграла. Сформулируем понятия верхней и нижней интегральных сумм

Сформулируем понятия верхней и нижней интегральных сумм. Пусть т_i – наименьшее значение функции f (x) на отрезке Δ x_i, а M_i – ее наибольшее значение на этом отрезке.

Определение 11.2. Сумма s_n = 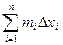называется нижней интегральной суммой функции f (x) на [ a,b ], а S_n = 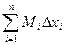- верхней интегральной суммой.

Свойства интегральных сумм.

1. Так как на любом отрезке разбиения m_i ≤ M_i, то s_i ≤ S_i.

2. Если т – наименьшее значение f(x) на [ a,b ], а М – ее наибольшее значение на [ a,b ], то .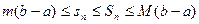

3. При добавлении к выбранному разбиению новых точек s_n может только возрастать, а S_n – только уменьшаться.

Доказательство.

Пусть отрезок [ x_k-1,x_k ] разбит на р отрезков. Обозначим нижнюю и верхнюю интегральные суммы на этих отрезках как s_p и S_p. Но для отрезка [ x_k-1,x_k ] наименьшим значением функции является т_к, а наибольшим – М_к. Следовательно, по свойству 2 s_p ≥ m_k Δ x_k – соответствующему слагаемому общей интегральной суммы s, а S_k≤ M_k Δ x_k – слагаемому верхней интегральной суммы. Таким образом, каждое слагаемое s может только увеличиваться при добавлении новых точек, а каждое слагаемое S – только уменьшаться, что и доказывает сформулированное утверждение.

1. Существуют 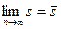и .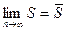

Доказательство.

Из свойств 2 и 3 следует, что s ограничена (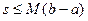) и монотонно возрастает. Следовательно, она имеет предел. Подобное же рассуждение справедливо для S.

1. Если f (x) непрерывна на [ a,b ], то .

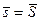Доказательство.

Назовем колебанием функции f (x) на отрезке Δ х_к разность ω_k = M_k – m_k. Тогда в силу непрерывности f (x) 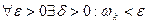при 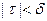. Следовательно, 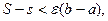то есть 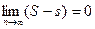, что и требовалось доказать.

Замечание. Так как s и S можно считать частными случаями интегральных сумм функции f (x), то =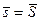

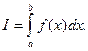
1. Для любых двух разбиений данного отрезка τ₁ и τ₂ .

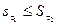Для доказательства этого утверждения достаточно рассмотреть разбиение, включающее все точки разбиений τ₁ и τ₂, и воспользоваться свойствами 1 и 3.

Перечислим основные свойства определенного интеграла.

1. Постоянный множитель можно выносить за знак интеграла:

.

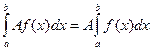Доказательство.

=

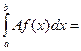
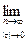
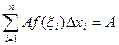
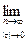
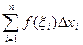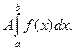
2. .

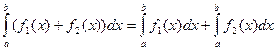Доказательство.

= ( + ) =

= .

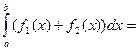
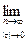
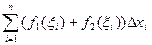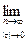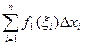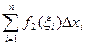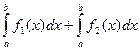3.Если на отрезке [ a,b ] (a<b) f (x) ≤ g (x), то .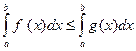

Доказательство.

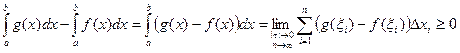, так как 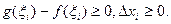Отсюда следует, что .

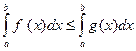у А ₂ В ₂ Геометрическая интерпретация:

площадь криволинейной трапеции аА ₁ В ₁ b не

больше площади аА ₂ В ₂ b.

A ₁ B ₁

a b

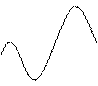
4. Если т и М – наименьшее и наибольшее значения функции f(x) на отрезке [ a,b ], 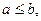то

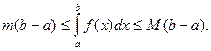
Доказательство.

Так как 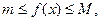по свойству 3 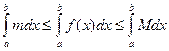. Но 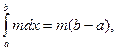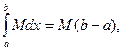следовательно,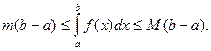

у А ₂ В ₂ Геометрическая интерпретация:

площадь криволинейной трапеции содержится

М между площадями прямоугольников aA ₁ B ₁ b и

aA ₂ B ₂ b.

А ₁ т В ₁

а b

5 (Теорема о среднем). Если функция f(x) непрерывна на отрезке [ a,b ], то на этом отрезке найдется такая точка ξ, что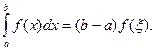

Доказательство.

Пусть 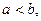т и М – наименьшее и наибольшее значения функции f(x) на [ a,b ]. Тогда по свойству 4 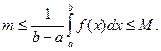Тогда 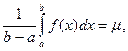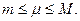Так как f(x) непрерывна на [ a,b ], она принимает на нем все промежуточные значения между т и М, то есть существует 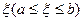такое, что 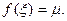Тогда 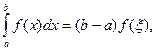что и требовалось доказать.

1. Для любых трех чисел a,b,c справедливо равенство

,

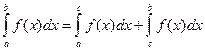если все эти интегралы существуют.

Доказательство.

Пусть a < c < b. Составим интегральную сумму так, чтобы точка с была точкой деления. Тогда 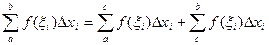. Переходя к пределу при 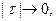получим доказательство свойства 6.

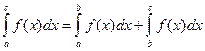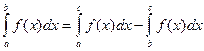Если a < b < c, то по только что доказанному , или . Но 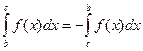, поэтому 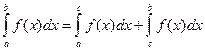. Аналогично доказывается это свойство и при любом другом расположении точек a, b и с.

Лекция 12.

Интегрируемость непрерывных, кусочно-непрерывных и монотонных ограниченных функций. Производная интеграла по переменному верхнему пределу. Формула Ньютона – Лейбница.

Теорема 12.1. Функция, непрерывная на отрезке, интегрируема на нем.

Доказательство.

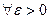
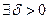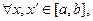
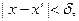
Если функция f(x) непрерывна на отрезке [ a,b ], то она, во-первых, ограничена на нем, а во-вторых, равномерно непрерывна, то есть такое, что 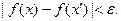Тогда для разбиения, в котором 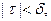колебание 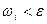, следовательно, 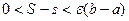, и по свойству 5 верхних и нижних интегральных сумм получим, что существует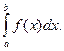

Теорема 12.2. Функция, монотонная на отрезке, интегрируема на нем.

Доказательство.

Пусть f(x) возрастает на [ a,b ]. Тогда 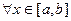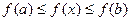, то есть f(x) ограничена на [ a,b ]. Кроме того, для любого интервала [ x_i-1, x_i ] 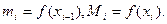Следовательно,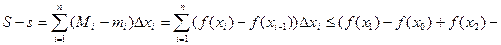

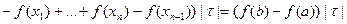. Поэтому 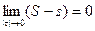, следовательно, f(x) интегрируема на [ a,b ].

Замечание. В теореме 12.2 не требовалась непрерывность функции. Монотонная функция может быть и разрывной, при этом она является интегрируемой по теореме 12.2.

Теорема 12.3. Если f(x) – непрерывная функция и 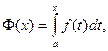то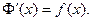

(Производная от определенного интеграла по верхнему пределу равна подынтегральной функции, в которую вместо переменной интегрирования подставлено значение верхнего предела).

Доказательство.

Пусть Δ х – приращение аргумента х. Тогда по свойству 6 определенного интеграла

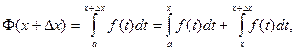
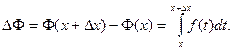
По теореме о среднем (свойство 5) 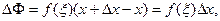где 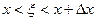. Поэтому 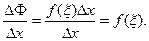Следовательно, 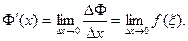Но при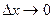

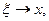и вследствие непрерывности функции f(x) 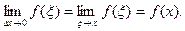Таким образом, 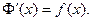Теорема доказана.

Замечание. Из теоремы 12.3 следует, что всякая непрерывная функция имеет первообразную, так как по теореме 12.1 она интегрируема, а по теореме 12.3 ее первообразной является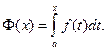

Теорема 12.4. Если F(x) является первообразной непрерывной функции f(x), то справедлива формула

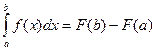, (12.1)

называемая формулой Ньютона – Лейбница.

Доказательство.

По теореме 12.3 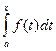- первообразная функции f(x), поэтому F(x) и 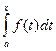отличаются на постоянное слагаемое С. Следовательно, 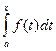= F(x) + C. (12.2)

Пусть х=а, тогда из (12.2) получим 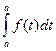= F(a) + C, то есть F(a) + C = 0, откуда

C = - F(a). Тогда 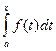= F(x) – F(a). Принимая в этом равенстве x=b, получим формулу Ньютона – Лейбница: .

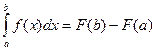Замечание. Обычно вводится обозначение 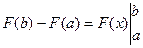, и формула (12.1) записывается так: .

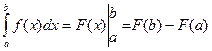Примеры.

1.

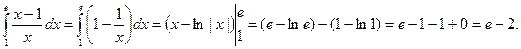
2.

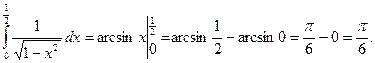
Лекция 13.

Замена переменной и интегрирование по частям в определенном интеграле. Применение определенного интеграла к вычислению площадей плоских фигур.

Теорема 13.1. Если:

1) функция f(x) непрерывна на отрезке [ a,b ],

2) функция φ(t) непрерывна и имеет непрерывную производную φ΄(t) на отрезке [α,β], где a = φ(α), b = φ(β),

3) функция f (φ(t)) определена и непрерывна на отрезке [α,β],

то 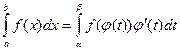. (13.1)

Доказательство.

Если F(x) – первообразная для f(x), то ,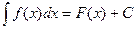

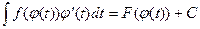(см. теорему 6.2). Тогда, используя формулу Ньютона – Лейбница, получим: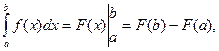 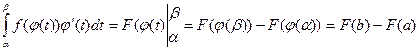, откуда следует справедливость формулы (13.1).

Замечание. В отличие от неопределенного интеграла, в определенном интеграле нет необходимости возвращаться к прежней переменной интегрирования, так как результатом вычисления будет число, не зависящее от выбора переменной.

Пример.

Вычислить интеграл 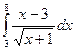. Сделаем замену: 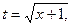откуда 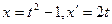. При этом 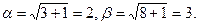Тогда =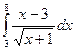

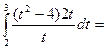
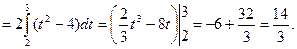
Теорема 13.2. Если функции u(x) и v(x) непрерывны вместе со своими производными на отрезке [ a,b ], то

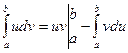. (13.2)

(Формула (13.2) называется формулой интегрирования по частям для определенного интеграла).

Доказательство.

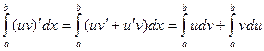. Все интегралы в этом равенстве существуют, так как подынтегральные функции непрерывны. При этом 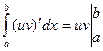, поэтому 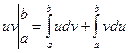, откуда следует (13.2).

Примеры.

1. Вычислить интеграл 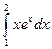. Пусть u = x, dv = e^xdx. Тогда du = dx, v = e^x. Применим формулу (13.2): .
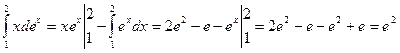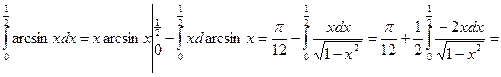
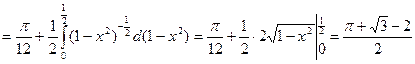2. . (При интегрировании принималось u = x, v = arcsin x).
3. Вычислить 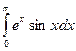. Пусть u = e^x, dv = sin xdx. Тогда du = e^xdx, v = - cos x. Следовательно, 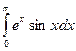= 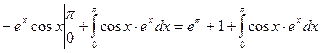. Применим к интегралу в правой части полученного равенства еще раз формулу интегрирования по частям, положив u = e^x, dv = cos xdx: 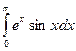= 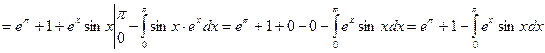. Поскольку при этом в правой части равенства стоит такой же интеграл, как в левой, его значение можно найти из уравнения: 2 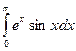= e^π + 1, то есть

=

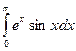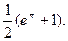
Геометрические приложения определенного интеграла.

1. Вычисление площадей плоских фигур.

Вспомним, каким образом вводилось понятие определенного интеграла. С геометрической точки зрения интегральная сумма представляет собой (при f(x) ≥ 0) сумму площадей прямоугольников с основанием 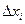и высотой 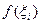. Переходя к пределу при |τ|→0, получаем, что 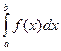при 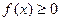представляет собой площадь так называемой криволинейной трапеции aА₁В₁b, то есть фигуры, ограниченной частью графика функции

у

у

y=f(x) y=f₂(x)

A ₁ B ₁

y=f₁(x)

a b х a b x

Рис. 1 Рис. 2

f(x) от х = а до x = b и отрезками прямых х = а, x = b и у = 0 (рис. 1):

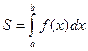. (13.3)

Если требуется найти площадь фигуры, ограниченной графиками двух функций: f₁(x) и f₂(x) (рис. 2), то ее можно рассматривать как разность площадей двух криволинейных трапеций: верхней границей первой из них служит график функции f₂(x), а второй – f₁(x). Таким образом, 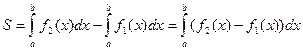. (13.4)

Замечание 1. Формула (13.4) справедлива, если графики функций f₁(x) и f₂(x) не пересекаются при a < x < b.

Замечание 2. Функции f₁(x) и f₂(x) могут при этом принимать на интервале [ a,b ] значения любого знака.

Пример.

Найти площадь фигуры, ограниченной графиками функций y = x ² - 3 x – 5 и y = x – 5.

Найдем абсциссы точек пересечения указанных графиков, то есть корни уравнения x ² - 3 x – 5 = x – 5. x ² - 4 x = 0, x ₁ = a = 0, x ₂ = b = 4. Таким образом, найдены пределы интегрирования. Так как на интервале [0,4] прямая y = x – 5 проходит выше параболы у = x ² - 3 x – 5, формула (13.4) примет вид: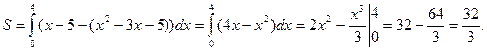

Лекция 14.