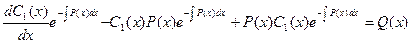
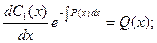
Из этого уравнения определим переменную функцию С1(х):
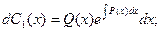
Интегрируя, получаем:
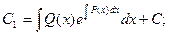
Подставляя это значение в исходное уравнение, получаем:

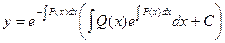 .
.
Таким образом, мы получили результат, полностью совпадающий с результатом расчета по методу Бернулли.
При выборе метода решения линейных дифференциальных уравнений следует руководствоваться простотой интегрирования функций, входящих в исходный интеграл.
Далее рассмотрим примеры решения различных дифференциальных уравнений различными методами и сравним результаты.
Пример. Решить уравнение 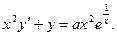
Сначала приведем данное уравнение к стандартному виду: 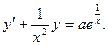
Применим полученную выше формулу: 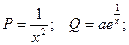
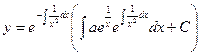
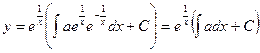
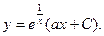
Уравнение Бернулли.
Определение. Уравнением Бернулли называется уравнение вида
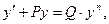
где P и Q – функции от х или постоянные числа, а n – постоянное число, не равное 1.
Для решения уравнения Бернулли применяют подстановку 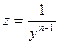 , с помощью которой, уравнение Бернулли приводится к линейному.
, с помощью которой, уравнение Бернулли приводится к линейному.
Для этого разделим исходное уравнение на yn.
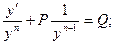
Применим подстановку, учтя, что 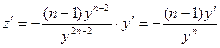 .
.
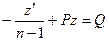
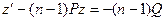
Т.е. получилось линейное уравнение относительно неизвестной функции z.
Решение этого уравнения будем искать в виде:

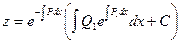

Пример. Решить уравнение 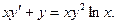
Разделим уравнение на xy2: 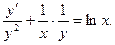
Полагаем 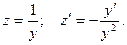
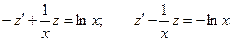 .
.
Полагаем 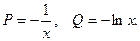
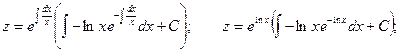
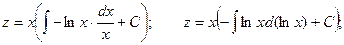
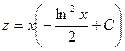
Произведя обратную подстановку, получаем:
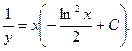
Пример. Решить уравнение 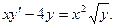
Разделим обе части уравнения на 
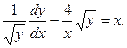
Полагаем 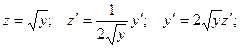
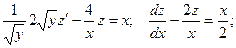
Получили линейное неоднородное дифференциальное уравнение. Рассмотрим соответствующее ему линейное однородное уравнение:
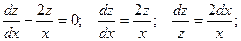
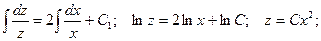
Полагаем C = C(x) и подставляем полученный результат в линейное неоднородное уравнение, с учетом того, что:
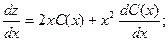
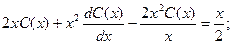
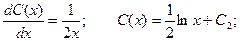
Получаем: 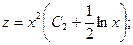
Применяя обратную подстановку, получаем окончательный ответ:
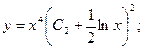
 2014-02-03
2014-02-03 1289
1289