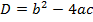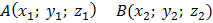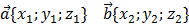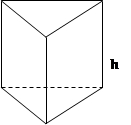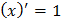Формулы сокращенного умножения
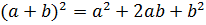
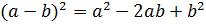
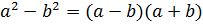
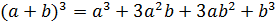
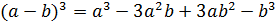
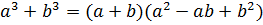
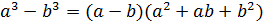
Решение квадратного уравнения 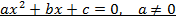
|
| 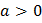 | Ветви вверх |
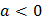 | Ветви вниз | |
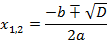 | 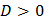 | 2 точки пересечения с осью ОX |
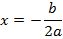 | 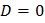 | 1 точка пересечения с осью ОX (вершина параболы) |
| нет корней | 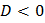 | нет точек пересечения с осью ОX |
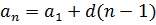
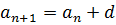

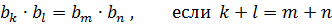
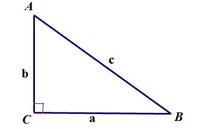
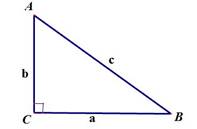 | Теорема Пифагора 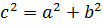 |
 | 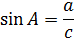 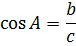 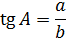 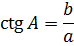 |
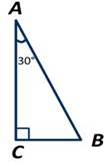 | 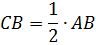 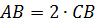 |
Многоугольники
| Квадрат | 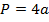 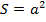 |
| Прямоугольник | 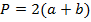 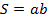 |
| Параллелограмм | 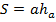 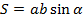 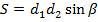 |
| Ромб | 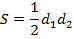 |
| Трапеция | 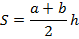 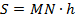 , , 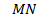 – средняя линия – средняя линия |
| Треугольник | 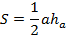 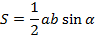 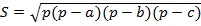 , где , где 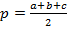 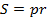 , где r –радиус вписанной окружности , где r –радиус вписанной окружности 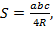 где где 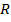 – радиус описанной окружности – радиус описанной окружности 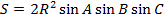 РАВНОСТОРОННИЙ ТРЕУГОЛЬНИК: РАВНОСТОРОННИЙ ТРЕУГОЛЬНИК: 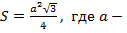 сторона треугольника ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК: сторона треугольника ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК: 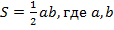 - катеты - катеты |
| Теорема синусов | 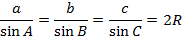 |
| Теорема косинусов | 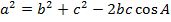 |
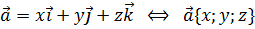
|
| |
| Координаты вектора AB | 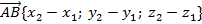 |
| Координаты середины отрезка AB | 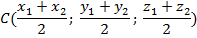 |
| Расстояние между точками А и В | 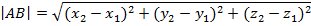 |
|
| |
| Длина вектора | 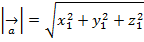 |
| Cумма векторов | 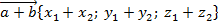 |
| Умножение вектора на число | 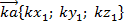 |
| Определение скалярного произведения векторов | 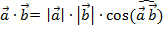 |
| Скалярное произведение векторов в координатах | 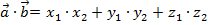 |
| Косинус угла между векторами | 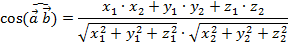 |
Многогранники
Прямоугольный параллелепипед
| 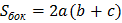 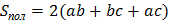 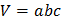 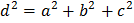 | |||
Призма прямая
| 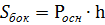 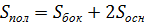 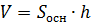 | |||
Пирамида правильная
| 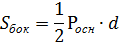 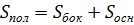 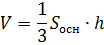 |
Тела вращения
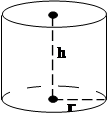
Цилиндр
| 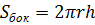 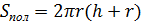 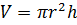 | |||
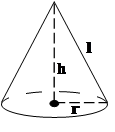
Конус
| 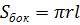 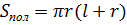 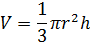  | |||
| Уравнение сферы | 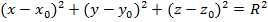 где где 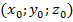 – центр сферы – центр сферы 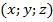 – точка с поверхности сферы – точка с поверхности сферы 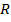 – радиус сферы – радиус сферы | |||
Сфера, шар 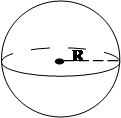 | 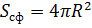 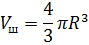 | |||
| Длина окружности | 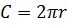 | |||
| Площадь круга | 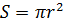 |
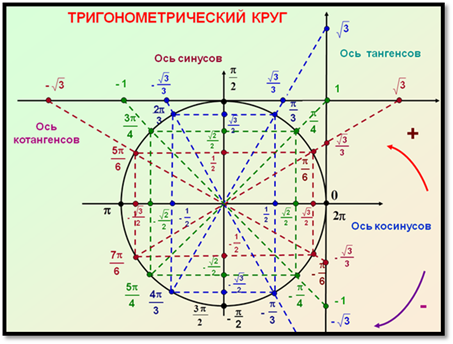
Тригонометрия
Тригонометрический круг
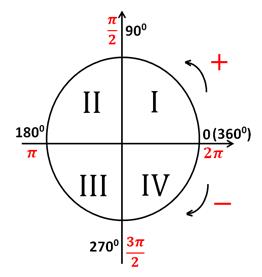
Единичная окружность – окружность с центром в точке (0;0) и r =1
Знаки тригонометрических функций
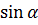 | 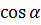 | 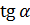 и и 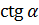 |
 |  |  |
Свойства тригонометрических функций
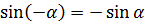
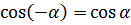
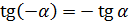
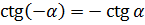
|
| 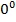 | 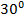 | 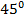 | 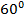 | 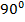 | 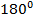 | 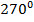 | 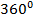 |
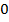 | 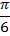 | 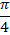 | 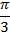 | 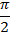 | 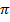 | 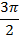 | 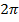 | |
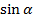 | 0 |  | 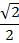 | 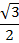 | 1 | 0 | -1 | 0 |
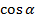 | 1 | 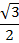 | 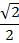 |  | 0 | -1 | 0 | 1 |
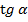 | 0 | 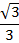 | 1 | 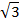 | – | 0 | – | 0 |
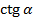 | – | 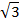 | 1 | 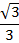 | 0 | – | 0 | – |
Значения тригонометрических функций
Графики тригонометрических функций
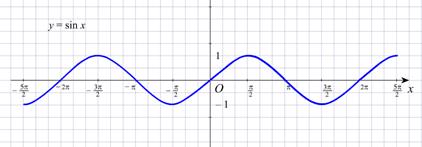
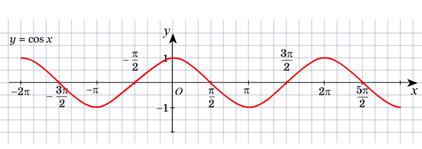
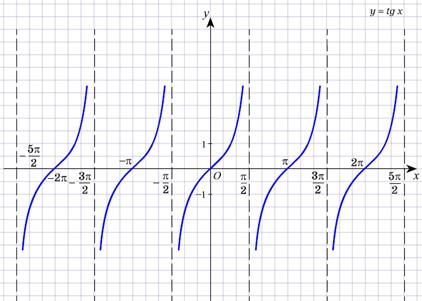
Основные тождества
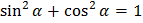
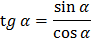
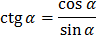
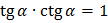
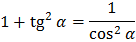
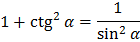
Формулы приведения
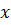 | 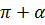 | 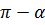 | 2 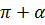 | 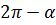 |
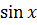 | 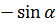 | 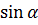 | 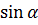 | 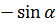 |
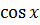 | 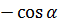 | 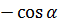 | 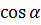 | 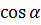 |
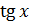 | 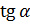 | 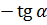 | 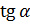 | 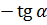 |
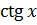 | 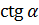 | 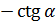 | 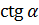 | 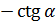 |
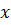 | 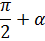 | 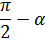 | 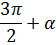 | 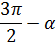 |
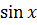 | 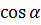 | 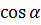 | 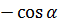 | 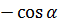 |
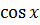 | 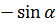 | 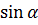 | 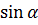 | 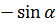 |
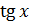 | 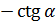 | 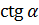 | 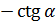 | 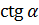 |
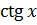 | 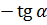 | 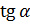 | 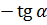 | 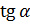 |
Формулы сложения
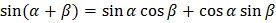
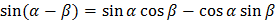
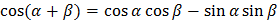
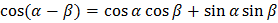
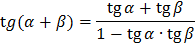
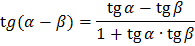
Формулы двойного угла
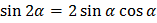
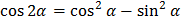
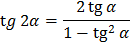
Формулы половинного угла
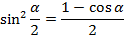
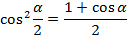
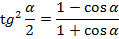
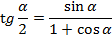
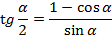
Формулы суммы и разности
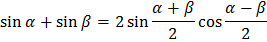
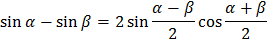
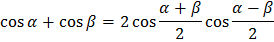
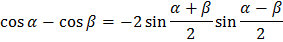
Решение простейших тригонометрических уравнений
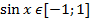
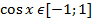
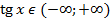
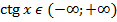
Пусть а – положительное число
| Уравнение | Решение |
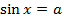 | 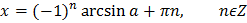 |
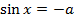 | 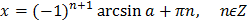 |
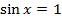 | 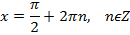 |
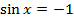 | 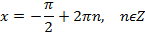 |
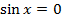 | 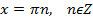 |
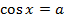 | 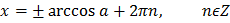 |
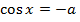 | 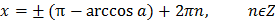 |
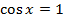 | 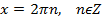 |
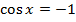 | 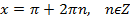 |
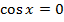 | 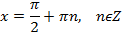 |
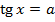 | 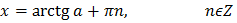 |
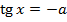 | 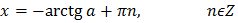 |
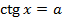 | 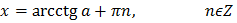 |
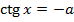 | 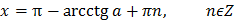 |
Производная
Правила вычисления производных
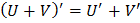
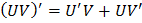
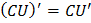
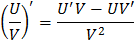
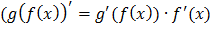
Таблица производных
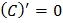
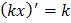
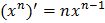
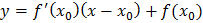
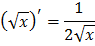
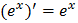
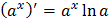

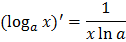
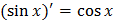
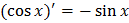
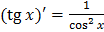
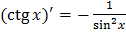
Геометрический смысл производной 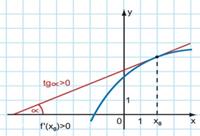 | 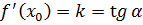 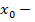 точка касания, точка касания, 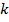 – угловой коэффициент касательной, – угловой коэффициент касательной, 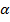 – угол наклона касательной – угол наклона касательной |
Физический смысл производной 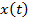 – закон движения, – закон движения, 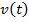 – скорость движения, – скорость движения, 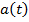 – ускорение движения – ускорение движения | 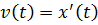 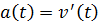 |
| Достаточное условие монотонности функции | 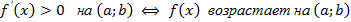 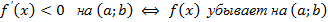 |
Достаточное условие экстремума непрерывной в точке 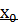 функции функции 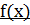 | «Если при переходе через точку 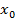 производная меняет знак с «+» на «-», то производная меняет знак с «+» на «-», то 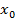 – точка максимума» «Если при переходе через точку – точка максимума» «Если при переходе через точку 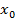 производная меняет знак с «-» на «+», то производная меняет знак с «-» на «+», то 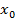 – точка минимума» – точка минимума» |
Таблица первообразных
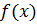 | 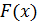 |
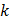 | 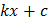 |
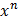 | 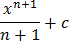 |
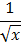 | 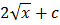 |
 | 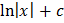 |
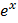 | 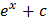 |
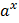 | 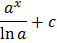 |
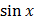 | 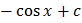 |
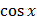 | 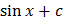 |
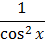 | 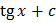 |
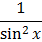 | 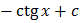 |
Криволинейная трапеция 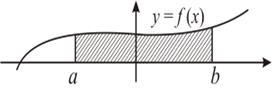
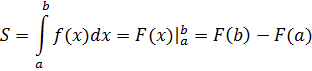
Свойства корней
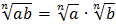
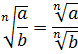
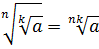
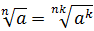
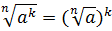
Если 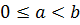 , то
, то 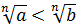
Свойства степеней
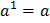
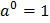
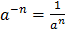
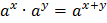
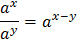
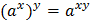
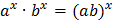
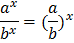
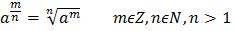
Таблицы степеней
| n | 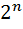 | 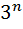 |
| 1 | 2 | 3 |
| 2 | 4 | 9 |
| 3 | 8 | 27 |
| 4 | 16 | 81 |
| 5 | 32 | 243 |
| 6 | 64 | 729 |
| 7 | 128 | 2187 |
| 8 | 256 | 6561 |
| 9 | 512 | 19683 |
| 10 | 1024 | 59049 |
| n | 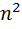 |
| 11 | 121 |
| 12 | 144 |
| 13 | 169 |
| 14 | 196 |
| 15 | 225 |
| 16 | 256 |
| 17 | 289 |
| 18 | 324 |
| 19 | 361 |
| 20 | 400 |
| 21 | 441 |
| 22 | 484 |
| 23 | 529 |
| 24 | 576 |
| 25 | 625 |
| n | 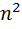 | 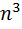 |
| 1 | 1 | 1 |
| 2 | 4 | 8 |
| 3 | 9 | 27 |
| 4 | 16 | 64 |
| 5 | 25 | 125 |
| 6 | 36 | 216 |
| 7 | 49 | 343 |
| 8 | 64 | 512 |
| 9 | 81 | 729 |
| 10 | 100 | 1000 |
Логарифмы
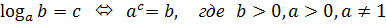
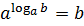 – основное логарифмическое тождество
– основное логарифмическое тождество
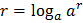 – представление числа
– представление числа 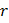 в виде логарифма
в виде логарифма
Свойства логарифмов
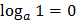
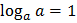
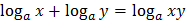
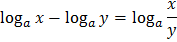
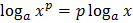
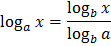
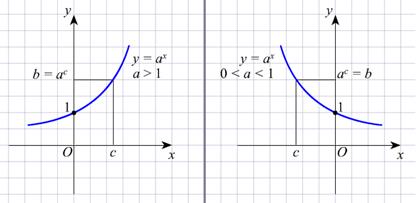
| График показательной функции |
 |
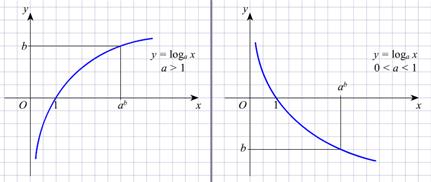
| График логарифмической функции |
 |
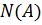 – число благоприятных исходов
– число благоприятных исходов
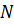 – число всевозможных исходов
– число всевозможных исходов
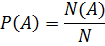
Перестановки, размещения, сочетания
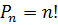
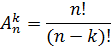
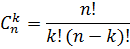
 2023-09-21
2023-09-21 1708
1708