2021-11-13
310
При расчете КИХ-фильтров методом частотной выборки задача формулируется так: необходимо составить уравнение и структуру цифрового фильтра, частотная характеристика которого задана N выборками (отсчетами). Возможный график АЧХ приведен на рис. 7.18.
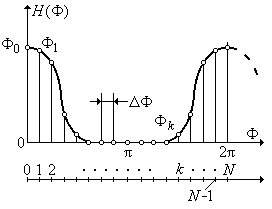
Рис. 7.18. Представление АЧХ КИХ-фильтра конечным числом отсчетов.
Отсчеты АЧХ эквидистантно размещены на периоде цифровых частот Ф = 0 … 2p. Интервал дискретизации по частоте DF выражается в виде:
DF = 2p/ N.
На рис. 7.18 наряду со шкалой цифровых частот F приведена шкала номеров интервалов k.
Частоты Ф k, на которых определяются выборки, выражаются следующим образом:
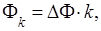(7.60)
k = 0, 1, 2, …, N – 1.
Дискретизированный комплексный коэффициент передачи КИХ-фильтра будем обозначать H (j F k).
ДИХ фильтра определим, используя выражения (7.31) и (7.34):
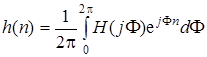, (7.61)
где H (j F) = H (F)exp[ j j(F)].
Поскольку в рассматриваемой задаче комплексный коэффициент передачи дискретизирован, то интеграл в (7.61) можно представить суммой, приняв d F = DF = 2p/ N:
В показателе экспоненты заменим F k на (2p/ N)· k. В результате получим:
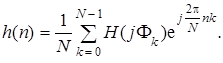(7.62)
Рассмотрение (7.62) показывает, что ДИХ h (n)является периодической бесконечной последовательностью с периодом N отсчетов, что следует из очевидного соотношения
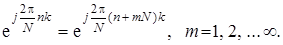
Прежде, чем делать выводы из такого формального заключения, составим выражение для H (j F k), как z -преобразование ДИХ при z = = exp(j F k):
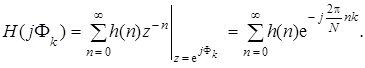(7.63)
Учитывая цикличность экспоненциальной функции в (7.63), при вычислении каждого значения H (j F k) (при k = 0, 1, 2,... N – 1) достаточно суммирование в (7.63) ограничить числом слагаемых, которые определяются только первым периодом последовательности h (n)в (7.62), т.е. верхний предел суммирования можно принять равным N – 1:
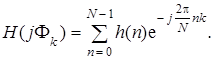(7.64)
Проведенное рассмотрение позволяет сделать важный вывод: цифровой фильтр, частотная характеристика которого задана N выборками в интервале частот 0…2p, имеет ДИХ в виде ограниченной последовательности, состоящей из N отсчетов. Следовательно, такой фильтр является КИХ-фильтром.
Соотношение (7.64) носит название прямого дискретного преобразования Фурье, сокращенно ДПФ, а (7.62) – обратного дискретного преобразования Фурье, сокращенно ОДПФ.
Передаточную функцию КИХ-фильтра представим, как z -преобразование его ДИХ:
(7.65)
Изменим в (7.65) порядок суммирования:
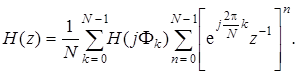(7.66)
Введем обозначение
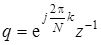(7.67)
и найдем вторую сумму в (7.66), как сумму N членов геометрической прогрессии со знаменателем q:
(7.68)
Подставив (7.68) в (7.66), получим:
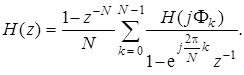(7.69)
Передаточная функция (7.69), содержащая комплексные коэффициенты, не может быть непосредственно использована для составления структуры физически реализуемого КИХ-фильтра. Однако форма записи (7.69) позволяет сразу установить общий признак этой структуры: она является последовательно-параллельной и формально может быть представлена структурной схемой на рис. 7.19.
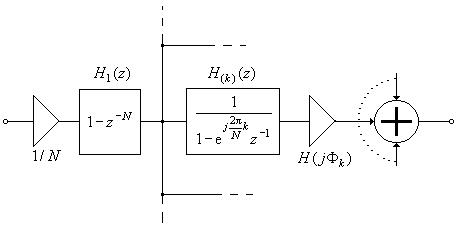
Рис. 7.19. Формальное представление структуры фильтра с передаточной функцией (7.69).
Выделим отдельный канал в этой схеме, состоящий из блоков с передаточными функциями H 1(z), H ( k )(z)и умножителя с коэффициентом 1/ N.
Блок с передаточной функцией
H 1(z) = 1 – z – N (7.70)
относится к физически реализуемому нерекурсивному фильтру, передаточная функция которого содержит N нулей z 0 k. Координаты нулей находятся из уравнения
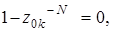(7.71)
где 1 = exp(j 2p k), k = 0, 1, 2, …, N – 1. Преобразуя (7.71), получаем:
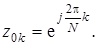(7.72)
Следовательно, все N нулей функции (7.70) расположены в равноотстоящих точках на окружности единичного радиуса с интервалом 2p/ N (рис. 7.20).
Блок на рис. 7.19 с передаточной функцией
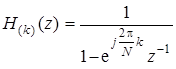(7.73)
обеспечивает только один полюс:
Положение полюса для k = 2 показано на рис. 7.20.
Рис. 7.20. Нуль-полюсная диаграмма КИХ-фильтра по схеме рис. 7.19.
Совмещение нуля и полюса в одной точке означает, что результирующая передаточная функция H рез(z) рассматриваемых двух блоков на частоте F = q при zk = z 0 k = z П k принимает конечное значение
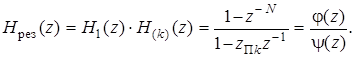(7.74)
Раскрывая неопределенность в (7.74) при zk = z 0 k = z П k, получим:
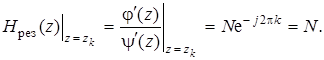
Таким образом, результирующий коэффициент передачи выделенных двух блоков и умножителя с коэффициентом 1/ N равен единице и, следовательно, частотная выборка H (j F k) = H (j q) воспроизводится на входе сумматора абсолютно точно. Полюсы передаточных функций остальных каналов не совпадают с нулем, имеющим угловую координату q. Следовательно, на частоте q коэффициенты передачи всех каналов, кроме рассматриваемого, равны нулю, а выборка H (j q) абсолютно точно воспроизводится и на выходе сумматора, т.е. на выходе КИХ-фильтра.
Общее заключение, вытекающее из проведенного рассмотрения, состоит в том, что КИХ-фильтр с передаточной функцией (7.69) обеспечивает абсолютно точное воспроизведение заданной частотной характеристики только на частотах дискретизации F k.
Для оценки качества аппроксимации заданной частотной характеристики между выборками H (j F k) составим выражение для реальной частотной характеристики КИХ-фильтра. Для этого в (7.69) введем замену z = exp(j F), тогда получим:
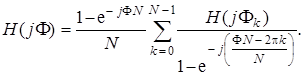(7.75)
Преобразуем комплексные разности в (7.75)
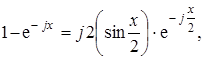
тогда
(7.76)
После преобразований (7.76) получим:
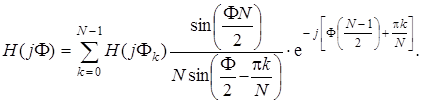(7.77)
Для практических расчетов функция (7.77) должна быть видоизменена в зависимости от конкретного варианта следующих условий:
1. Заданная АЧХ проектируемого КИХ-фильтра может быть как четной, так и нечетной функцией частоты.
2. Заданная ФЧХ в общем случае может не соответствовать линейной зависимости.
3. Число N интервалов разбиения частотной оси при определении выборок F k может быть как четным, так и нечетным.
4. Первую выборку F k (при k = 0) не обязательно производить на частоте Ф = 0. Например, если в составе входного сигнала постоянная составляющая отсутствует, то диапазон частот 0 … 2p можно дискретизировать так, как это показано на рис. 7.21.
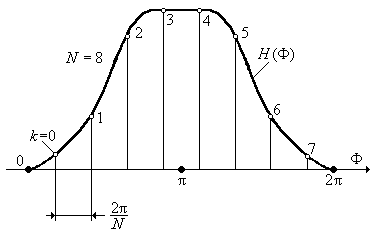
Рис. 7.21. Вариант дискретизации заданной АЧХ КИХ-фильтра.
Дальнейшее рассмотрение проведем, приняв следующие условия:
– будем считать, что заданная АЧХ симметрична относительно точки Ф = p, а ФЧХ должна быть линейной;
– число N интервалов частотной дискретизации примем нечетным, а первую выборку заданной АЧХ будем определять на частоте Ф = 0.
Поскольку ФЧХ линейна, фазовый множитель определяется выражением:
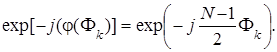
Подставив в последнее выражение F k = 2p k / N, получим:
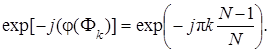(7.78)
Теперь выражение для H (j F k) можно записать в виде:
(7.79)
Введем (7.79) в (7.77):
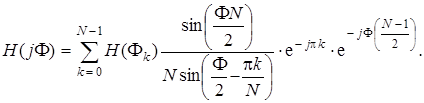(7.80)
Преобразуем содержащееся в (7.80) произведение sina×exp(– j p k):
sina×exp(– j p k) = sina×cosp k = sin(a - p k). (7.81)
С учетом (7.81) выражение (7.80) примет вид:
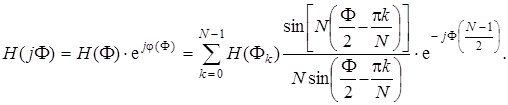(7.82)
Из (7.82) следует, в частности, что КИХ-фильтр, рассчитанный методом частотной выборки, сохраняет заданную линейность ФЧХ.
Перейдем к расчету АЧХ H (F) КИХ-фильтра в соответствии с принятыми условиями. Исходное выражение для H (F) следует из (7.82):
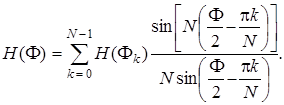(7.83)
Суммируемые члены в (7.83) можно разбить на три группы:
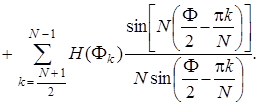(7.84)
В силу симметрии функции H (F k) относительно точки F = p можно записать:
H (F k) = H (F N - k). (7.85)
Соотношение (7.85) позволяет третью сумму в (7.84) определять в тех же пределах, что и вторую, но с заменой переменной k в синусных функциях на N - k:
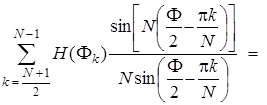
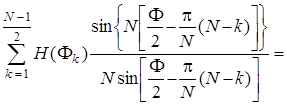
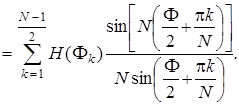(7.86)
Таким образом, вторая и третья суммы в (7.84) могут быть объединены в одну, и окончательное выражение для АЧХ рассчитываемого КИХ-фильтра примет следующий вид:
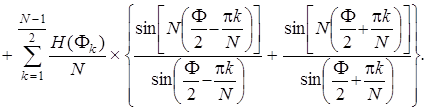(7.87)
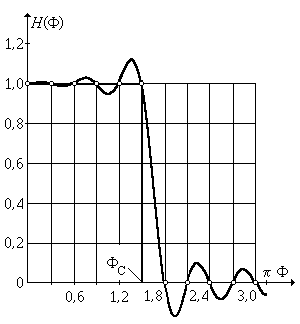
Рис. 7.22. Реальная АЧХ КИХ-фильтра.
На рис. 7.22 в качестве примера расчета по (7.87) показан график реальной АЧХ КИХ-фильтра нижних частот при заданной форме АЧХ в виде идеального прямоугольника (частота среза FC = 1,496; N = 21). Белыми кружочками показаны отсчеты идеальной АЧХ.
Наличие пульсаций и конечной (ненулевой) переходной зоны в графике реальной АЧХ являются уже известными нам признаками искажений АЧХ, свойственных КИХ-фильтрам.
Заметим, что увеличение N не приводит к уменьшению уровня пульсаций в форме АЧХ, а лишь повышает их частоту. Уменьшить уровень пульсаций можно расширением переходных зон в задаваемой форме АЧХ.
Важнейшим положением в проектировании КИХ-фильтров методом частотной выборки является рациональный выбор отсчетов АЧХ в заданной переходной зоне. Произвольный выбор этих отсчетов может привести к существенному увеличению интенсивности пульсаций в АЧХ. Поиск оптимальных значений частотных выборок в переходной зоне, обеспечивающих минимизацию пульсаций АЧХ, осуществляется машинным расчетом с помощью специально разработанных алгоритмов, познакомиться с которыми можно в [10].
Структурная схема КИХ-фильтра составляется, как известно, на основе передаточной функции H (z) с действительными коэффициентами. Считая по-прежнему, что N нечетное, а первая выборка производится на частоте F = 0, общее выражение (7.69) для H (z) преобразуем так, чтобы комплексные полюсы, определяемые знаменателями под знаком суммы, были бы объединены в сопряженные пары:
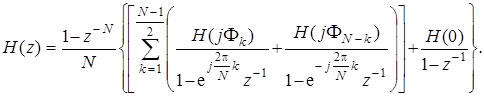(7.88)
При составлении (7.88) учитывалась как симметрия функции H (j F k) относительно точки F = p, так и симметричное расположение сопряженных полюсов в верхней и нижней z -полуплоскостях (рис. 7.20). Действительный полюс с координатами (+1, 0) учтен в (7.88) отдельным слагаемым. Таким образом, в (7.88) под одним и тем же номером k фигурируют две симметричных выборки H (j F k) и H (j F N - k) и два сопряженных полюса. При этом H (F k) = H (F N - k).
Как показано в подразделе 7.1 (выражение (7.18)), у рассматриваемого типа КИХ-фильтров ФЧХ антисимметрична:
j(F) = - j(2p - F).
Имея в виду отмеченные обстоятельства, можно составить следующие соотношения:
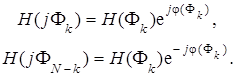(7.89)
Подставим (7.89) в (7.88):
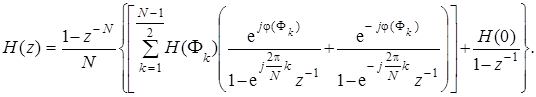(7.90)
После приведения выражения, стоящего в круглых скобках, к общему знаменателю и представления комплексных экспонент в тригонометрической форме, передаточная функция (7.90) преобразуется к следующему виду:
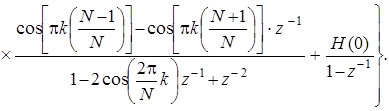(7.91)
Заметим, что cos[p k (N - 1)/ N ] = cos[p k (N + 1)/ N ], поэтому в окончательном виде выражение (7.91) можно представить так:
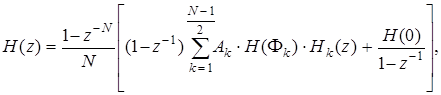(7.92)
где
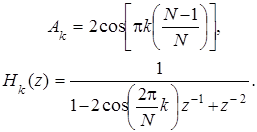(7.93)
Структурная схема КИХ-фильтра, составленная на основе (7.92), показана на рис 7.23.
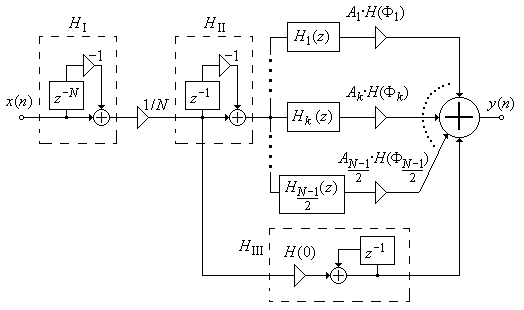
Рис. 7.23. Структурная схема КИХ-фильтра, реализованного методом частотной выборки.
Цифровые фильтры с передаточными функциями Hk (z), стоящие в параллельных ветвях на схеме рис. 7.23, являются чисто рекурсивными со структурой, изображенной на рис. 7.24.
Рис. 7.24. Структура рекурсивного фильтра.
Покажем, что, несмотря на наличие в структуре рис. 7.23 рекурсивных ветвей, ДИХ фильтра является конечной. Рассмотрим отдельные каналы, состоящие из последовательно включенных фильтров H I(z), Hk (z) и умножителя с коэффициентом AkH (F k). Передаточные функции Hk (z) в(7.93) содержат два комплексно-сопряженных полюса, расположенных на окружности единичного радиуса:
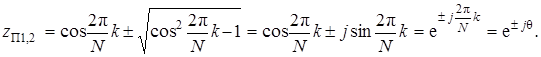
ДИХ блока с передаточной функцией (7.93) описывается выражением:
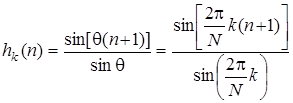(7.94)
(см. выражение (5.63) в главе 5) и представляет собой незатухающее гармоническое колебание.
Запишем разностное уравнение фильтра с передаточной функцией H II(z):
y (n) = x (n) - x (n - 1), (7.95)
следовательно, ДИХ выделенного канала с использованием (7.94) и (7.95) определится так:
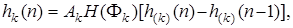
и после преобразований
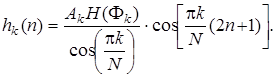(7.96)
Итак, отклик выделенного канала на единичный импульс представляет собой бесконечную периодическую последовательность hk (n),возбуждаемую в момент времени, соответствующий отсчету с номером n = 0.Период этой последовательности равен N отсчетам. В момент времени, соответствующий отсчету с номером n=N,из блока с передаточной функцией H II(z) на рис. 7.23 повторно поступает входной единичный импульс, задержанный на N тактов дискретизации, но с противоположной полярностью, что приводит к полной компенсации колебаний (7.96) после отсчета с номером n = N -1. Таким образом, ДИХ каждого канала в структуре рис 7.23 ограничены N отсчетами с номерами от 0 до N -1.
ДИХ последнего канала с передаточной функцией
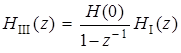
тоже является ограниченной последовательностью с N отсчетами, равными H (0).
Результирующая ДИХ КИХ-фильтра со структурой на рис 7.23 определяется суммированием ДИХ всех параллельных ветвей
(7.97)
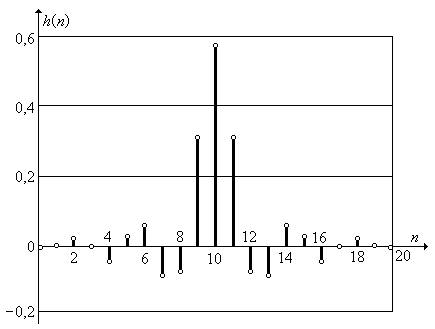
Рис. 7.25. ДИХ КИХ-фильтра.
На рис. 7.25 показана рассчитанная по (7.97) ДИХ КИХ-фильтра, АЧХ которого изображена на рис. 7.22.
Тот же результат расчета ДИХ можно получить, используя выражение для обратного преобразования Фурье (7.62), которое при четной АЧХ КИХ-фильтра с линейной ФЧХ записывается так:
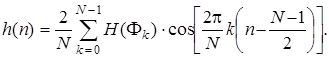(7.98)
В общем случае вычислительные алгоритмы КИХ-фильтров, спроектированных на основе методов частотной выборки и взвешивания, практически не отличаются по своей сложности.
Воспользуемся общепринятым способом определения сложности вычислительного алгоритма по оценке числа необходимых умножений, как наиболее медленных операций среди других (сложение, запоминание, обращение к памяти).
В методе взвешивания предусматривается N умножений на коэффициенты 
равные отсчетам взвешенной ДИХ. Число этих коэффициентов равно порядку фильтра.
Для подсчета числа умножений в алгоритме КИХ-фильтра на основе частотной выборки обратимся к структурным схемам на рис. 7.23 и 7.24. Очевидно, что в этом подсчете можно не учитывать операции умножения на -1, осуществляющие инверсию полярности обрабатываемых последовательностей. Тогда полное число умножений на коэффициенты 2cos(2p k / N), AkH (F k) и H (0) также равно порядку фильтра N.
Однако в ряде случаев значительная часть отсчетов при дискретизации АЧХ может быть принята равной нулю, что дает возможность существенно упростить структуры КИХ-фильтра с частотной выборкой за счет уменьшения числа каналов.
Мы рассмотрели многоканальную структуру фильтра, синтезированного методом частотной выборки. Ее можно преобразовать в одноканальную, используя другую запись для передаточной функции.
Общее выражение для передаточной функции многоканального ЦФ имеет вид:
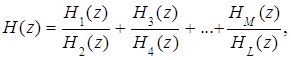(7.99)
где слагаемые представляют собой передаточные функции отдельных каналов. Приведем правую часть в (7.99) к общему знаменателю. Получающаяся при этом дробно-рациональная функция и является основой для создания одноканальной многокаскадной структуры ЦФ.
Заметим, что этот одноканальный ЦФ имеет достаточно высокий порядок, определяемый в первую очередь числом каналов исходной структуры. В результате время межтактовой обработки может существенно возрасти, что в свою очередь потребует уменьшения частоты дискретизации.
