Определения:
Направляющим вектором прямой называется вектор 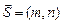 , который параллелен прямой или лежит на ней.
, который параллелен прямой или лежит на ней.
Нормальным вектором прямой называется вектор 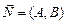 перпендикулярный этой прямой.
перпендикулярный этой прямой.
Угловым коэффициентом прямой называется число 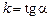 , где
, где 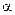 - угол между прямой и положительным направлением оси
- угол между прямой и положительным направлением оси 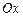 .
.
Понятно, что направляющий и нормальный векторы определяются неоднозначно. Все направляющие векторы коллинеарны между собой. Это же верно и для нормальных векторов. Угловой коэффициент к прямой определяется единственным образом (для прямых, перпендикулярных оси 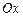 угловой коэффициент не определен).
угловой коэффициент не определен).
Рассмотренные три понятия 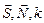 в определенном смысле характеризуют направление прямой. Зная некоторые данные относительно прямой, можно найти её уравнение.
в определенном смысле характеризуют направление прямой. Зная некоторые данные относительно прямой, можно найти её уравнение.
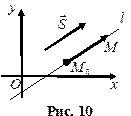 |
Дано: точка 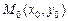 на прямой
на прямой 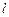 и направляющий вектор
и направляющий вектор 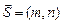 прямой (рис.10). Пусть
прямой (рис.10). Пусть 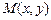 - произвольная точка прямой. Составим вектор
- произвольная точка прямой. Составим вектор 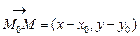 , который коллинеарен вектору
, который коллинеарен вектору 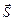 . Используя условие коллинеарности получим уравнение
. Используя условие коллинеарности получим уравнение
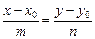 ,
,
которое называется каноническим уравнением прямой в 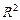 .
.
2.Дано:точка 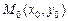 на прямой на прямой 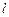 и нормальный вектор и нормальный вектор 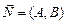 прямой (рис.11). Если прямой (рис.11). Если 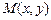 - произвольная точка прямой, то векторы - произвольная точка прямой, то векторы 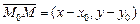 и и 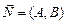 перпендикулярны. Записывая условие перпендикулярности векторов, получим уравнение перпендикулярны. Записывая условие перпендикулярности векторов, получим уравнение | 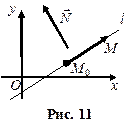 |
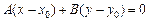 ,
,
которое называется уравнением прямой с нормальным вектором.
3.Дано:точка 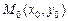 на прямой на прямой 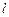 и угловой коэффициент и угловой коэффициент 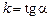 прямой (рис.12). Из рисунка видно, что вектор прямой (рис.12). Из рисунка видно, что вектор 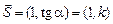 является направляющим вектором прямой. Каноническое уравнение прямой является направляющим вектором прямой. Каноническое уравнение прямой 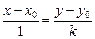 приводится к виду приводится к виду | 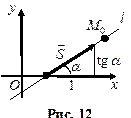 |
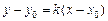 ,
,
которое называется уравнением прямой, проходящей через данную точку с данным угловым коэффициентом.
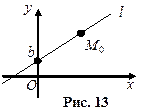 | 4.Дано: точка 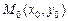 на прямой на прямой 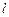 и отрезок и отрезок 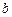 , отсекаемый прямой на оси , отсекаемый прямой на оси 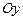 (рис.13). Преобразуем уравнение прямой (рис.13). Преобразуем уравнение прямой 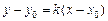 , получим , получим 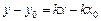 , ,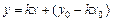 . Обозначим . Обозначим 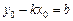 . . |
Тогда уравнение прямой примет вид 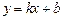 , и называется уравнением прямой с угловым коэффициентом. Таккак при
, и называется уравнением прямой с угловым коэффициентом. Таккак при 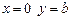 , то
, то 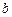 – это отрезок, отсекаемый прямой на оси
– это отрезок, отсекаемый прямой на оси 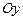 . Полученное уравнение прямой широко используется в приложениях. Для прямых перпендикулярных оси
. Полученное уравнение прямой широко используется в приложениях. Для прямых перпендикулярных оси 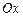 имеем
имеем 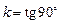 - не существует. Следовательно, для таких прямых не существует уравнений, содержащих угловой коэффициент
- не существует. Следовательно, для таких прямых не существует уравнений, содержащих угловой коэффициент 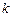 .
.
5. Дано: две точки 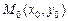 ,
,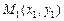 на прямой
на прямой 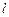 . Вектор
. Вектор 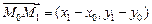 является направляющим вектором прямой. Каноническое уравнение прямой
является направляющим вектором прямой. Каноническое уравнение прямой
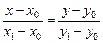
называется уравнением прямой в 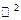 , проходящей через две точки.
, проходящей через две точки.
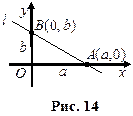 | 6. Дано: отрезки 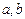 , отсекаемые прямой , отсекаемые прямой 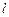 на осях координат на осях координат 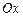 и и 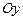 (рис.14). Так как точки (рис.14). Так как точки 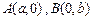 лежат на прямой, то, используя уравнение прямой, проходящей через две точки лежат на прямой, то, используя уравнение прямой, проходящей через две точки 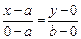 , получим уравнение , получим уравнение |
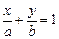 ,
,
которое называется уравнением прямой в отрезках.
Пример 4.1. Найти уравнения прямых, проходящих через точку 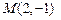 с:
с:
1) направляющим вектором 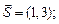
2) нормальным вектором 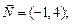
3) с угловым коэффициентом 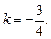
Решение. 1) Воспользуемся каноническим уравнением прямой с 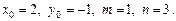 Получим
Получим

2) Воспользуемся уравнением прямой с нормальным вектором, где 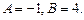
Получим
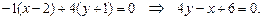
3) Воспользуемся уравнением прямой, проходящей через данную точку с данным угловым коэффициентом. Получим
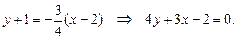
Пример 4.2. Найти уравнение прямой, проходящей через две точки 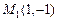 ,
, 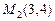 . Найти отрезки, отсекаемые прямой на осях координат.
. Найти отрезки, отсекаемые прямой на осях координат.
Решение. Воспользуемся уравнением прямой, проходящей через две точки
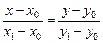 ,
,
где 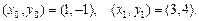 Получим
Получим
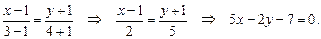
Преобразуем это уравнение к виду уравнения прямой в отрезках, получим
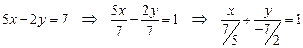 ,
,
то есть, 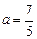 ,
, 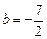 .
.
 2014-02-13
2014-02-13 1485
1485
