Даны векторы, заданные в координатах 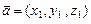 ,
, 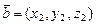 . Используя свойства 5, 6 скалярного произведения, составим таблицу (табл.1) значений скалярного произведения единичных векторов
. Используя свойства 5, 6 скалярного произведения, составим таблицу (табл.1) значений скалярного произведения единичных векторов 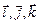 .
.
Таблица 1
 | 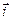 | 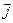 | 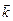 |
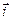 | |||
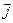 | |||
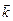 |
Отсюда имеем,
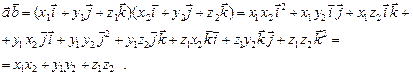
Итак, получена формула, выражающая скалярное произведение векторов в координатах
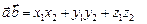 . (1)
. (1)
Пример 1.2 Дано: 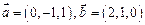 .
.
Найти: 1) 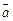
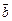 ;
;
2) 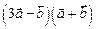 двумя способами.
двумя способами.
Решение. 1) Используя формулу (1)получим
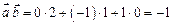 .
.
2) первый способ: раскроем скобки, пользуясь свойствами скалярного произведения,
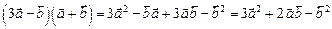 .
.
Так как 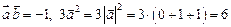
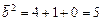 , то получим
, то получим 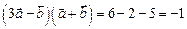
3) второй способ: найдем координаты сомножителей
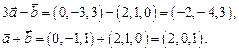
Тогда
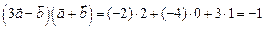 .
.
Геометрические и физические приложения скалярного произведения
1. Модуль вектора 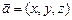 . В силу свойства 5 скалярного произведения
. В силу свойства 5 скалярного произведения 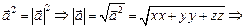
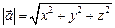 .
.
2. Угол 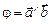 между векторами
между векторами 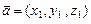 и
и 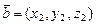 . Из определения скалярного произведения
. Из определения скалярного произведения 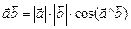
получим формулу 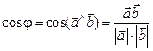 , (2)
, (2)
которая в координатах имеет вид
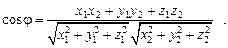
3. Условие перпендикулярности векторов 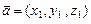 и
и 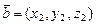 .
.
Из свойства 6 скалярного произведения 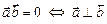 получим условие перпендикулярности векторов
получим условие перпендикулярности векторов
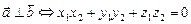 .
.
4. Расстояние 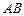 между точками
между точками 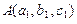 и
и 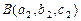 .
.
Так как 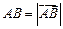 и
и 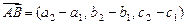 , то
, то
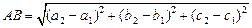 .
.
Физическая задача.Под действием постоянной силы 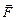 материальная точка перемещается прямолинейно из материальная точка перемещается прямолинейно из 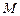 в в 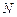 (рис.1). Из физики известно, что работу совершают только составляющая силы (рис.1). Из физики известно, что работу совершают только составляющая силы 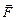 , направленная по линии перемещения. , направленная по линии перемещения. | 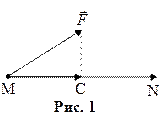 |
Работа 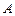 равна произведению длины составляющей на длину перемещения
равна произведению длины составляющей на длину перемещения
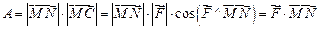 .
.
Пример 1.3. Даны вершины треугольника 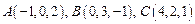 . Найти угол при вершине А.
. Найти угол при вершине А.
Решение. Составим два вектора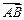 и
и 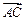 с общим началом-точкой А. Получим
с общим началом-точкой А. Получим
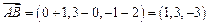 ,
,
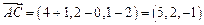 .
.
Найдем косинус угла А, как косинус угла между векторами 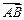 и
и 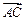
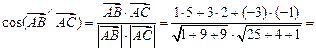
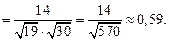
Следовательно,
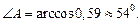
Пример 1.4. Найти работу силы 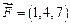 , затраченную на прямолинейное перемещение материальной точки из
, затраченную на прямолинейное перемещение материальной точки из 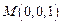 в
в 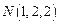 .
.
Решение. Найдем координаты вектора 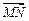
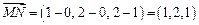 .
.
Найдем работу А, как скалярное произведение вектора силы 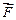 на вектор перемещения
на вектор перемещения 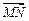 , получим
, получим
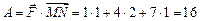 (Дж).
(Дж).
 2014-02-13
2014-02-13 1982
1982
