Или.
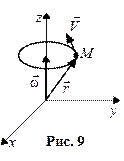
Связь линейной и угловой скоростей.Если материальная точка 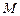 вращается вокруг неподвижной оси с угловой скоростью вращается вокруг неподвижной оси с угловой скоростью 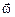 (рис.9), то линейная скорость (рис.9), то линейная скорость 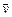 равна векторному произведению угловой скорости равна векторному произведению угловой скорости 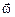 на радиус - вектор на радиус - вектор 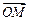 точки точки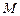
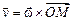 или или 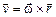 . .
| 
|
Пример 2.3. Найти площадь треугольника АВС, если известны его вершины 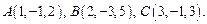
Решение. Воспользуемся формулой площади треугольника через координаты векторов 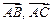
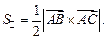
Для этого найдем координаты векторов
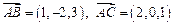 и их векторное произведение
и их векторное произведение
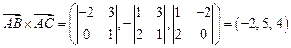 .
.
Так как
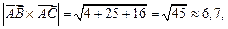
то площадь треугольника равна
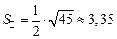 (кв.ед).
(кв.ед).
Пример 2.4. Найти вектор 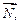 перпендикулярный плоскости, в которой лежат три точки
перпендикулярный плоскости, в которой лежат три точки 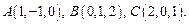
Решение. Если вектор 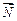 перпендикулярен плоскости, то он перпендикулярен любым прямым, лежащим на плоскости, в частности, векторам
перпендикулярен плоскости, то он перпендикулярен любым прямым, лежащим на плоскости, в частности, векторам 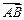 и
и 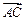 . Это значит, что в качестве вектора
. Это значит, что в качестве вектора 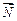 можно взять векторное произведение
можно взять векторное произведение 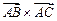 . Таким образом,
. Таким образом, 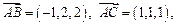
то 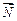 =
=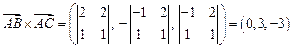 .
.
 2014-02-13
2014-02-13 373
373








