Рассмотрим несколько задач.
Задача 1. Найти угол 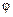 между прямыми между прямыми 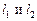 (рис.15). Решение. При вычислении мы можем найти острый угол (рис.15). Решение. При вычислении мы можем найти острый угол 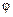 или дополнительный к нему тупой угол или дополнительный к нему тупой угол 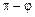 . Для нахождения угла . Для нахождения угла 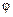 получим несколько формул, в зависимости от данных относительно уравнения прямой. получим несколько формул, в зависимости от данных относительно уравнения прямой.
| 
|
а) известны угловые коэффициенты 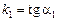 ,
, 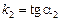 прямых
прямых 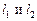 . Так как
. Так как 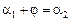 , то
, то 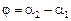 , а значит
, а значит 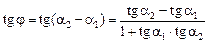 , следовательно
, следовательно
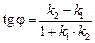 .
.
б) Известны направляющие векторы 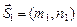 ,
, 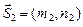 прямых
прямых 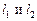 . Тогда
. Тогда 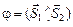 , а значит
, а значит
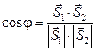 .
.
в) Известны нормальные векторы 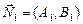 ,
,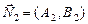 прямых
прямых 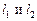 . Тогда
. Тогда 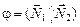 , а значит
, а значит
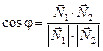 .
.
Задача 2. Найти условие параллельности прямых 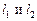 .
.
Решение. Прямые параллельны 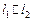 тогда и только тогда, когда:
тогда и только тогда, когда:
а) 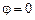 , т.е.
, т.е. 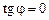 и
и 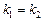 ;
;
б) 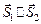 , т.е.
, т.е. 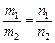 ;
;
в) 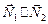 , т.е.
, т.е. 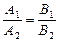 .
.
Задача 3. Найти условие перпендикулярности прямых 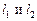 .
.
Решение. Прямые перпендикулярны 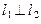 тогда и только тогда, когда:
тогда и только тогда, когда:
а) 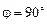 , т.е.
, т.е. 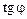 - не существует
- не существует 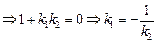 ;
;
б) 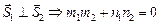 ;
;
в) 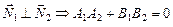 .
.
Задача 4. Найти точку пересечения прямых 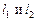 .
.
Решение. Из уравнений прямых 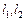 составим систему
составим систему 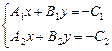 , решим ее. Решение системы
, решим ее. Решение системы 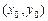 - точка пересечения прямых.
- точка пересечения прямых.
Пример 4.4. Найти угол между прямыми 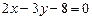 ,
, 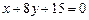 .
.
Решение. Угол 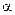 между прямыми равен углу между нормальными векторами к этим прямым:
между прямыми равен углу между нормальными векторами к этим прямым:
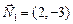 ,
, 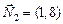 .
.
Следовательно,
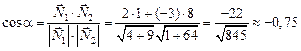 .
.
Знак 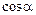 определяет величину угла, если
определяет величину угла, если 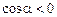 , то значит найден тупой угол
, то значит найден тупой угол 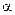 . Острый угол соответствует положительному значению косинуса.
. Острый угол соответствует положительному значению косинуса.
Следовательно,
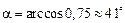 - острый угол,
- острый угол,
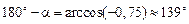 - тупой угол.
- тупой угол.
Пример 4.5. Найти уравнения прямых, проходящих через точку 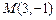 и:
и:
1) параллельно прямой 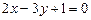 ;
;
2) перпендикулярно прямой 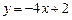 ;
;
3) под углом 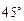 к
к 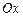 .
.
Решение. Чтобы найти уравнения прямых, надо воспользоваться условиями параллельности и перпендикулярности прямых:
1) найдем нормальный вектор данной прямой 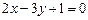
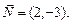
Так как искомая прямая параллельна данной прямой, то вектор 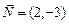 является нормальным для искомой прямой. Используя уравнение прямой с нормальным вектором, получим
является нормальным для искомой прямой. Используя уравнение прямой с нормальным вектором, получим
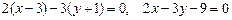 ;
;
2) найдем угловой коэффициент данной прямой 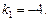 Из условия перпендикулярности прямых
Из условия перпендикулярности прямых 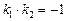 находим угловой коэффициент искомой прямой
находим угловой коэффициент искомой прямой
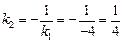 .
.
Найдем уравнение искомой прямой
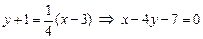 ;
;
3) найдем угловой коэффициент искомой прямой
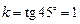 .
.
Следовательно,
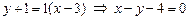 - уравнение искомой прямой.
- уравнение искомой прямой.
 2014-02-13
2014-02-13 520
520








