Общее уравнение прямой. Теорема 3.1) Любая прямая в определяется уравнением первой степени относительно текущих координат; 2) любое уравнение первой степени определяет прямую в

Теорема 3. 1) Любая прямая в 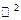определяется уравнением первой степени относительно текущих координат; 2) любое уравнение первой степени 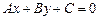определяет прямую в .

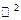Определение. Уравнение 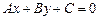называется общим уравнением прямой в 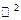. Это уравнение имеет первую степень относительно 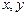(линейное уравнение), поэтому прямая называется линией первого порядка. Из общего уравнения легко найти все характеристики направления прямой:

1) 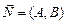- нормальный вектор;

2) т.к. 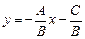, то 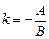- угловой коэффициент;

3) т.к. 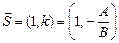, то вектор 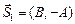является направляющим вектором прямой.

Пример 4.3. Стороны угла заданы уравнениями

, .

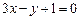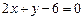Найти точку пересечения прямых.

Решение. Точка пересечения прямых находится как решение системы уравнений

.

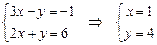Точка 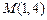- точка пересечения прямых.