Три вектора 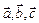 называются компланарными, если они лежат в одной плоскости (рис.2).
называются компланарными, если они лежат в одной плоскости (рис.2).
Тройка некомпланарных векторов 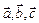 , приведенных к общему началу, называется правой, если из конца вектора
, приведенных к общему началу, называется правой, если из конца вектора 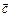 видно, что кратчайший поворот от вектора
видно, что кратчайший поворот от вектора 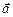 к вектору
к вектору 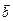 происходит против часовой стрелки (рис.3). Если кратчайший поворот от вектора
происходит против часовой стрелки (рис.3). Если кратчайший поворот от вектора 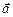 к вектору
к вектору 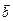 виден из конца вектора
виден из конца вектора 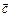 по часовой стрелке, то тройка
по часовой стрелке, то тройка 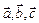 называется левой (рис.4).
называется левой (рис.4).

| 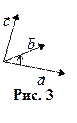
| 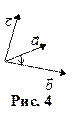
|
Примеры правых троек 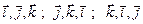 ;
;
примеры левых троек 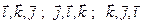 .
.
Векторным произведениемвекторов 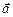 и и 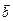 называется вектор называется вектор 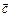 (рис.5), удовлетворяющий трем условиям:
1) (рис.5), удовлетворяющий трем условиям:
1) 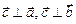 ;
2) ;
2) 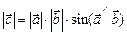 ,
3) ,
3) 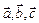 - правая тройка. - правая тройка.
| 
|
Обозначение векторного произведения: 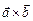 или
или 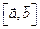 .
.
Примеры: 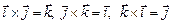 .
.
Свойства векторного произведения:
1) 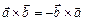 ;
;
2) 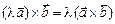 ;
;
3) 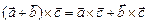 ;
;
4) 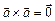 , так как
, так как 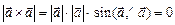 ;
;
5) Теорема 2. Векторное произведение двух ненулевых векторов равно нулевому вектору 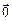 тогда и только тогда, когда векторы коллинеарны
тогда и только тогда, когда векторы коллинеарны
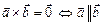 .
.
Пример 2.1. Найти 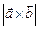 ,
, 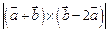 ,
,
если 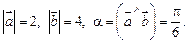
Решение. В силу определения векторного произведения имеем
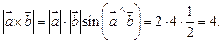
Пользуясь свойствами векторного произведения, получим
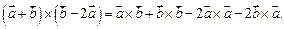
Так как 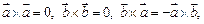 то
то 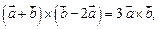 а значит
а значит
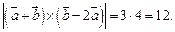
 2014-02-13
2014-02-13 673
673








