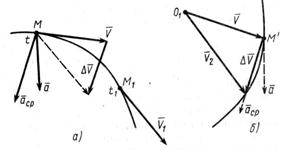
Пусть движущаяся точка М в момент времени t имеет скорость 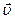 . В момент времени
. В момент времени 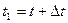 эта точка занимает положение М1, имея скорость
эта точка занимает положение М1, имея скорость 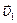 (рис. 4,а). Чтобы изобразить приращение скорости
(рис. 4,а). Чтобы изобразить приращение скорости 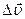 за время
за время 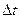 , перенесем вектор скорости
, перенесем вектор скорости 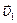 параллельно самому себе в точку М.
параллельно самому себе в точку М.
Средним ускорением точки 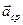 за время
за время 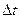 называют отношение
называют отношение 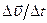 , т. е.
, т. е. 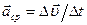 .
.
Ускорением точки 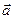 в момент времени t называют предел, к которому стремится среднее ускорение при
в момент времени t называют предел, к которому стремится среднее ускорение при 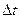 , стремящемся к нулю, т. е.
, стремящемся к нулю, т. е.
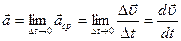 .
.
 Таким образом, ускорение точки равно первой производной по времени от скорости точки.
Таким образом, ускорение точки равно первой производной по времени от скорости точки.
Приращение скорости 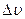 и, следовательно, среднее ускорение направлены внутрь вогнутости траектории. Так же направлены и их предельные значения при
и, следовательно, среднее ускорение направлены внутрь вогнутости траектории. Так же направлены и их предельные значения при 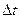 , стремящемся к нулю. Поэтому ускорение точки направлено тоже внутрь вогнутости траектории. Кроме того, ускорение как первая производная по времени от скорости, по свойству годографа вектора, параллельна касательной к годографу вектора скорости (рис. 4, 6).
, стремящемся к нулю. Поэтому ускорение точки направлено тоже внутрь вогнутости траектории. Кроме того, ускорение как первая производная по времени от скорости, по свойству годографа вектора, параллельна касательной к годографу вектора скорости (рис. 4, 6).
 Скорость точки направлена по касательной к траектории и вычисляется, согласно ее определению, по формуле
Скорость точки направлена по касательной к траектории и вычисляется, согласно ее определению, по формуле
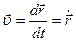 .
.
Для ускорения точки соответственно имеем
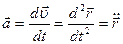 .
.
Векторный способ ввиду его краткости и компактности удобен для теоретического изложения кинематики точки.
 2014-02-17
2014-02-17 764
764







