Равномерное движение.
Частные случаи движения точки
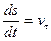
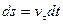
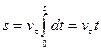
если принять при t = 0, s = 0
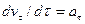
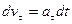
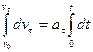
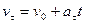 (*)
(*)
Так как 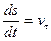 , то с учетом (*)
, то с учетом (*)
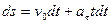
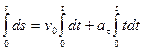
если при t = 0, s = 0. Выполняя интегрирование, получим
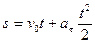
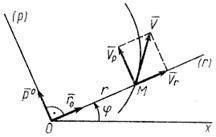 Примем какую-либо точку О плоскости за полюс и проведем из неё полярную ось, например ось Ох (рис. 10). Положение движущейся точки М на плоскости известно, если заданы радиус-вектор r и полярный угол
Примем какую-либо точку О плоскости за полюс и проведем из неё полярную ось, например ось Ох (рис. 10). Положение движущейся точки М на плоскости известно, если заданы радиус-вектор r и полярный угол 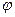 как функции времени, т. е.
как функции времени, т. е.
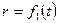
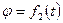 (1)
(1)
Полярный угол считается положительным, если он откладывается от полярной оси до радиуса - вектора против часовой стрелки. Радиус-вектор как расстояние от точки О до точки М принимает только положительные значения.
 Уравнения (1) называются уравнениями движения точки в полярных координатах. Они являются также уравнениями траектории точки в параметрической форме. Если из (1) исключить параметр - время t, то получим уравнение траектории в полярных координатах:
Уравнения (1) называются уравнениями движения точки в полярных координатах. Они являются также уравнениями траектории точки в параметрической форме. Если из (1) исключить параметр - время t, то получим уравнение траектории в полярных координатах:
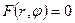
Введем единичный вектор 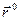 , направленный по радиусу-вектору от полюса О к точке М. Тогда
, направленный по радиусу-вектору от полюса О к точке М. Тогда
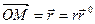
Для скорости 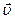 получаем
получаем
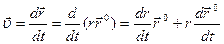
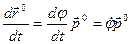
Где вместо единичного вектора 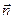 введён единичный вектор
введён единичный вектор 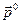 , направление которого получается поворотом вектора
, направление которого получается поворотом вектора 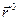 на
на 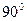 в положительном направлении угла
в положительном направлении угла 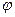 , т.е. против часовой стрелки (рис. 10). После этого для скорости точки получаем
, т.е. против часовой стрелки (рис. 10). После этого для скорости точки получаем
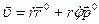
Это разложение скорости точки на радиальную 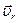 и трансверсальную (поперечную)
и трансверсальную (поперечную) 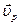 составляющие, т.е.
составляющие, т.е. 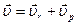
где
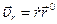 ,
, 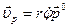
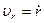 ,
, 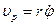
Определим ускорение точки в полярных координатах. Имеем
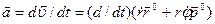
Выполняя дифференцирование, получаем
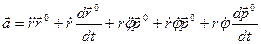
Для производной по времени от единичного вектора 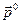 имеем
имеем
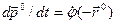 ,
,
Так как вектор 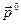 поворачивается с той же угловой скоростью
поворачивается с той же угловой скоростью 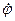 , что и вектор
, что и вектор 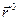 , а единичным вектором, по которому направлен вектор
, а единичным вектором, по которому направлен вектор 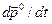 , является вектор
, является вектор 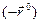 .
.
После подстановки в выражение для ускорения производных от единичных векторов и объединения слагаемых имеем
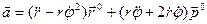 .
.
Получили разложение ускорения точки на радиальную 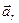 и трансверсальную
и трансверсальную 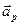 составляющие, т.е.
составляющие, т.е.
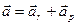 ,
, 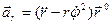 ,
, 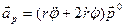 .
.
Для проекций ускорения на оси Or и Op получаем
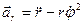 ,
, 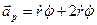 .
.
Ускорение 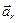 называется радиальным, а
называется радиальным, а 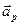 - трансверсальным. Трансверсальное
- трансверсальным. Трансверсальное ускорение можно выразить также в форме
ускорение можно выразить также в форме
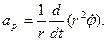
Радиальная и трансверсальная составляющие ускорения взаимно перпендикулярны, поэтому
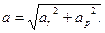
 2014-02-17
2014-02-17 3622
3622








