Задание движения и траектория
КООРДИНАТНЫЙ СПОСОБ ИЗУЧЕНИЯ ДВИЖЕНИЯ
Движение точки в декартовых координатах считается заданным, если известны координаты точки как непрерывные, дважды дифференцируемые функции времени, т. е. заданы уравнения движения точки в декартовых координатах:
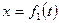 ;
; 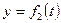 ;
; 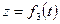 .
.
Эти уравнения движения есть также уравнения траектории точки в параметрической форме. Параметром является время t. Уравнения траектории в координатной форме получают исключением параметра t.
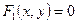 ,
, 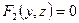 .
.
Разложим радиус-вектор и скорость точки на составляющие, параллельные осям координат. Получим
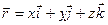 ;
; 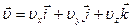 , (1)
, (1)
где х, у, z -координаты точки М; 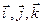 - единичные векторы осей координат;
- единичные векторы осей координат; 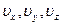 - проекции скорости на оси координат.
- проекции скорости на оси координат.
Учитывая (1), согласно определению скорости, имеем
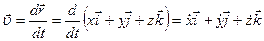 , (2)
, (2)
так как 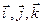 не изменяются при движении точки М. Точки над х, у, z означают их производные по времени. Сравнивая (1) и (2), получаем для проекций скорости на декартовы оси координат следующие формулы:
не изменяются при движении точки М. Точки над х, у, z означают их производные по времени. Сравнивая (1) и (2), получаем для проекций скорости на декартовы оси координат следующие формулы:
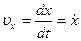 ;
; 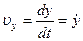 ;
; 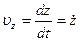 .
.
Проекция скорости точки на какую-либо координатную ось равна первой производной по времени от соответствующей координаты этой точки. По проекциям определяют числовое значение (модуль) скорости и косинусы углов вектора скорости с осями координат:
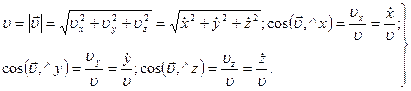
 2014-02-17
2014-02-17 2877
2877
