Разложим ускорение точки на составляющие, параллельные осям декартовой системы координат. Получим
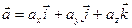 , (3)
, (3)
где 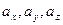 - проекции ускорения на координатные оси. Согласно определению ускорения и формулам (1) и (2), имеем
- проекции ускорения на координатные оси. Согласно определению ускорения и формулам (1) и (2), имеем
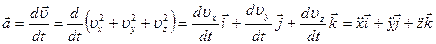 (4)
(4)
Сравнивая (3) и (4), получаем формулы для проекций ускорения на оси декартовой системы координат:
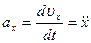 ;
; 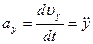 ;
; 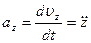 .
.
Проекция ускорения на какую-либо координатную ось равна второй производной по времени от соответствующей координаты движущейся точки.
Числовое значение ускорения и косинусы углов вектора ускорения с осями координат определяем по формулам
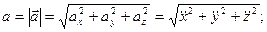
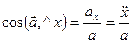 ;
; 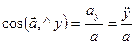 ;
; 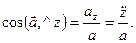
 2014-02-17
2014-02-17 776
776








