 Радиус кривизны и соприкасающаяся плоскость. В точке М кривой линии проведем касательную
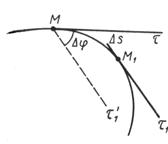
Радиус кривизны и соприкасающаяся плоскость. В точке М кривой линии проведем касательную 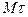 (рис. 6). В другой близкой точке кривой М1, отстоящей от точки М на расстоянии
(рис. 6). В другой близкой точке кривой М1, отстоящей от точки М на расстоянии 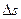 , построим касательную
, построим касательную 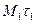 . В общем случае пространственной кривой касательные
. В общем случае пространственной кривой касательные 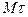 и
и 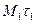 будут скрещиваться. Проведем в точке М прямую линию
будут скрещиваться. Проведем в точке М прямую линию 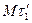 , параллельную
, параллельную 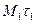 . Угол
. Угол 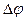 между линиями
между линиями 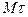 и
и 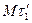 называется углом смежности. Кривизной кривой k в точке М называют предел, к которому стремится угол смежности, приходящийся на единицу расстояния
называется углом смежности. Кривизной кривой k в точке М называют предел, к которому стремится угол смежности, приходящийся на единицу расстояния 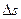 , причем
, причем 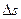 стремится к нулю, т. е.
стремится к нулю, т. е.

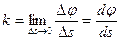
Радиусом кривизны кривой r в точке М называют величину, обратную кривизне кривой в этой точке, т. е.
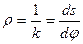
Для определения понятия соприкасающейся плоскости проводим вспомогательную плоскость через две пересекающиеся прямые 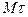 и
и 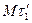 (см. рис. 6). Предельное положение этой плоскости при совпадении в пределе точки М1 с точкой М называется соприкасающейся плоскостью кривой в точке М.
(см. рис. 6). Предельное положение этой плоскости при совпадении в пределе точки М1 с точкой М называется соприкасающейся плоскостью кривой в точке М.
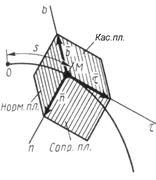 Естественный трехгранник. Построим в точке М кривой линии естественные оси этой кривой (рис. 7). Первой естественной осью является касательная
Естественный трехгранник. Построим в точке М кривой линии естественные оси этой кривой (рис. 7). Первой естественной осью является касательная 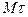 . Ее положительное направление совпадает с направлением единичного вектора касательной
. Ее положительное направление совпадает с направлением единичного вектора касательной 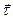 , направленного в сторону возрастающих расстояний.
, направленного в сторону возрастающих расстояний.
Перпендикулярно касательной 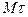 располагается нормальная плоскость кривой. Нормаль, расположенная в соприкасающейся плоскости, называется главной нормалью Мп. Она является линией пересечения нормальной плоскости с соприкасающейся плоскостью. По главной нормали внутрь вогнутости кривой направим единичный вектор п.
располагается нормальная плоскость кривой. Нормаль, расположенная в соприкасающейся плоскости, называется главной нормалью Мп. Она является линией пересечения нормальной плоскости с соприкасающейся плоскостью. По главной нормали внутрь вогнутости кривой направим единичный вектор п.
 Нормаль, перпендикулярная главной нормали, называется бинормалью. Единичный вектор
Нормаль, перпендикулярная главной нормали, называется бинормалью. Единичный вектор 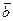 , направленный по бинормали так, чтобы три вектора
, направленный по бинормали так, чтобы три вектора 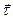 ,
, 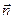 и
и 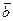 образовывали правую систему осей координат, определит положительное направление третьей естественной оси.
образовывали правую систему осей координат, определит положительное направление третьей естественной оси.
Три взаимно перпендикулярные оси 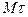 , Мп и Мb называются естественными осями кривой. Эти оси образуют в точке М естественный трехгранник. При движении точки по кривой естественный трехгранник движется вместе с точкой как твердое тело, поворачиваясь вокруг вершины, совпадающей с движущейся точкой.
, Мп и Мb называются естественными осями кривой. Эти оси образуют в точке М естественный трехгранник. При движении точки по кривой естественный трехгранник движется вместе с точкой как твердое тело, поворачиваясь вокруг вершины, совпадающей с движущейся точкой.
 Дифференцирование единичного вектора. Вычислим производную от единичного вектора по скалярному аргументу. Производная
Дифференцирование единичного вектора. Вычислим производную от единичного вектора по скалярному аргументу. Производная 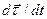 перпендикулярна самому единичному вектору
перпендикулярна самому единичному вектору 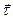 . Для доказательства этого используем тождество
. Для доказательства этого используем тождество

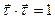
Дифференцируя по времени обе части этого тождества, получим
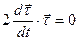
 Каждый из сомножителей этого выражения не равен нулю, поэтому векторы
Каждый из сомножителей этого выражения не равен нулю, поэтому векторы 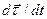 и
и 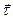 перпендикулярны друг другу.
перпендикулярны друг другу.
Направим по вектору 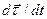 единичный вектор
единичный вектор 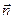 . Тогда
. Тогда
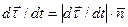 (*)
(*)
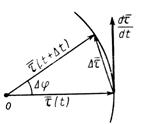
Годографом вектора 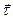 является кривая, расположенная на сфере единичного радиуса, так как единичный вектор изменяется только по направлению (рис. 8).
является кривая, расположенная на сфере единичного радиуса, так как единичный вектор изменяется только по направлению (рис. 8).
По определению модуля производной от вектора имеем

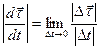
Длина малой хорды 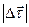 с точностью до малых величин более высокого порядка равна длине дуги, которую стягивает хорда, т. е.
с точностью до малых величин более высокого порядка равна длине дуги, которую стягивает хорда, т. е.
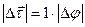
где 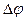 - угол, опирающийся на эту дугу. Используя это выражение, получим
- угол, опирающийся на эту дугу. Используя это выражение, получим
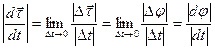
Подставляя это значение в (*) и используя выражение для радиуса кривизны и переменную s, получим
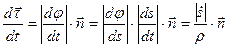
Радиус кривизны 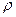 считаем положительным.
считаем положительным.
Ускорение точки при естественном способе задания движения
Учитывая, что для скорости точки имеем
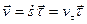
а в соответствии с определением ускорения получаем
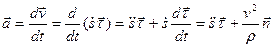
так как 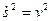 и
и 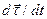 направлен внутрь вогнутости траектории параллельно единичному вектору главной нормали
направлен внутрь вогнутости траектории параллельно единичному вектору главной нормали 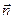 .
.
Получено разложение ускорения точки по осям естественного трехгранника. Часть ускорения
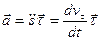
называется касательной составляющей ускорения. Другая часть ускорения
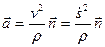
называется нормальной составляющей ускорения. Она направлена внутрь вогнутости траектории, т. е. в сторону положительного направления единичного вектора главной нормали 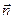 , так как внутрь вогнутости траектории направлено полное ускорение. Таким образом, ускорение точки
, так как внутрь вогнутости траектории направлено полное ускорение. Таким образом, ускорение точки
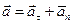 (*)
(*)
 Получим формулы для проекций ускорения на естественные оси. Имеем:
Получим формулы для проекций ускорения на естественные оси. Имеем:
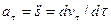
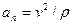
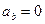
Проекция ускорения нa положительное направление касательной, совпадающее с направлением единичного вектора 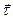 , называется касательным ускорением, а на главную нормаль, направленную по единичному вектору
, называется касательным ускорением, а на главную нормаль, направленную по единичному вектору 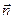 , -нормальным ускорением. Проекция ускорения на бинормаль, направленную по единичному вектору
, -нормальным ускорением. Проекция ускорения на бинормаль, направленную по единичному вектору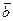 , равна нулю; следовательно, ускорение точки расположено в соприкасающейся плоскости траектории.
, равна нулю; следовательно, ускорение точки расположено в соприкасающейся плоскости траектории.
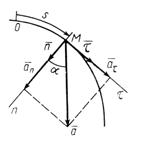
 Учитывая ортогональность
Учитывая ортогональность 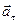 и
и 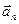 (рис. 9), в соответствии с уравнением (*) имеем
(рис. 9), в соответствии с уравнением (*) имеем
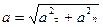
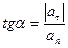
Нормальная составляющая ускорения 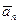 всегда направлена внутрь вогнутости траектории. Касательная составляющая
всегда направлена внутрь вогнутости траектории. Касательная составляющая 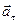 при
при 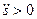 направлена в положительную сторону касательной, т. е. по направлению единичного вектора
направлена в положительную сторону касательной, т. е. по направлению единичного вектора 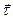 , а при
, а при 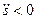 – в отрицательную, противоположно
– в отрицательную, противоположно 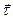 .
.
 2014-02-17
2014-02-17 4630
4630








