Смешанное произведение. Определение. Смешанным произведением трех векторов называется число

Определение. Смешанным произведением трех векторов называется число .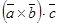

Применяя свойства векторного и скалярного произведения, можно получить формулу:

=,

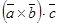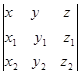где .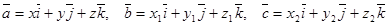

Так как

=,

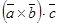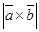
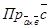где величина 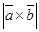равна площади параллелограмма, построенного на векторах – сторонах 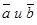, а величина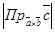равна высоте параллелепипеда, построенного на векторах – сторонах , то объем параллелепипеда вычисляется по формуле V =.

Пример. Вычислить объем пирамиды АBСD по ее вершинам А(1;1;0), В(0;2;4), С(-1;3;2), D(4;0;2).

Решение. Сначала находим векторы .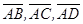

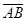=(0-1;2-1;4-0)=(-1;1;4), 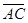=(-1-1;3-1;2-0)=(-2;2;2),

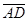=(4-1;0-1;2-0)=(3;-1;2).

Затем находим смешанное произведение векторов.

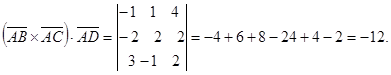
Потом находим объем параллелепипеда, построенного на векторах – сторонах .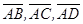

V =

Так как объем пирамиды равен шестой части объема параллелепипеда, то ее объем равен 2.