2014-02-09
1206
1. 
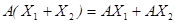, т.е. образ суммы векторов равен сумме образов каждого из них.
2. 
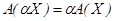, т.е. если вектор умножить на число, то его образ умножится на это число.
3. Если векторы коллиниарны, то их образы также коллиниарны, т.е. если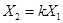 
, то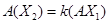 
, или иначе, линейное преобразование векторного пространства сохраняет коллиниарность (параллельность) векторов. Следовательно, образом параллелограмма будет так же параллелограмм.
4. Линейное преобразование векторного пространства сохраняет пропорциональность отрезков, т.е. если
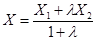, то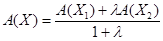 
.
Эти свойства легко следуют из соответствующих линейных операций над матрицами.
5. Площадь образа параллелограмма равна площади исходного параллелограмма, умноженной на абсолютную величину определителя матрицы линейного преобразования.
Доказательство. Пусть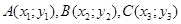 
- последовательные вершины исходного параллелограмма 
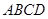, тогда его площадь равна
,
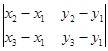где
= (
; 
), 
= (
; 
).
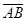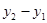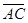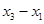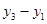Образом параллелограмма при линейном отображении с помощью матрицы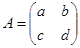 
является параллелограмм 
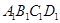со смежными сторонами-векторами
= (
()
();
()+
());
= (()();()+()).
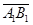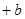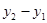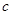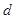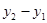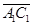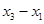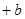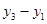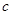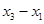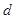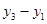Вычислим его площадь.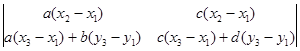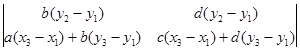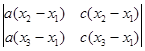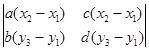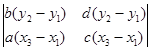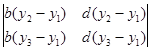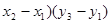
=
+
+
=
=
+ 
+
+ 
+ 
=
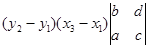= 0 + (
+ 
+ 0 =
= (
- 
=
=((- 
) =
=
.
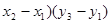
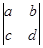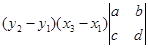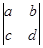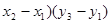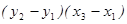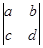
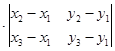Таким образом, свойство 5 доказано.
6. Объем образа параллелепипеда равен объему исходного параллелепипеда, умноженного на абсолютную величину определителя матрицы линейного преобразования.
Это свойство доказывается точно так же, как свойство 5.
