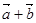Линейные операции над векторами
Сначала под вектором будем понимать величину, которая характеризуется числом и направлением. В последующем дадим обобщение этого понятия. Примерами векторов являются скорость, ускорение, сила, направленный отрезок и др. Направленный отрезок (геометрический вектор) является наглядным изображением таких векторов.
Два вектора называются коллинеарными, если они расположены на одной прямой или на параллельных прямых.
Два вектора называются равными, если они коллинеарные, одинаково направлены (сонаправлены) и имеют одинаковую длину (модуль).
Длина вектора  обозначается символом
обозначается символом 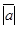 . Символом
. Символом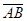 обозначается вектор, началом и концом которого служат точки А и В соответственно. Если векторы
обозначается вектор, началом и концом которого служат точки А и В соответственно. Если векторы  и
и 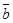 коллинеарные, то пишут:
коллинеарные, то пишут: 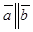 .
.
Сложение векторов выполняется по правилу параллелограмма или по правилу треугольника:
|
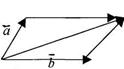
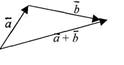
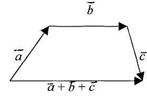
Для того чтобы сложить два и более векторов, надо образовать цепь, состоящую из этих векторов так, чтобы конец
первого вектора совпал с началом второго вектора, конец второго вектора совпадал с началом третьего вектора и т.д.
|
|
|
Вектор, замыкающий эту цепь, будет суммой этих векторов.
Нулевой вектор 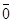 – это точка, или вектор с нулевой длиной, считается, что он имеет любое направление.
– это точка, или вектор с нулевой длиной, считается, что он имеет любое направление.
Разностью векторов  и
и 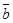 называется вектор
называется вектор 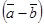 , который в сумме с вектором
, который в сумме с вектором 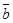 составляет вектор
составляет вектор  , т.е.
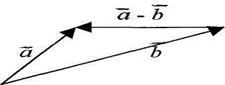
, т.е. 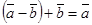 . Вычитание векторов можно производить по правилу треугольника:
. Вычитание векторов можно производить по правилу треугольника:
Произведением числа k на вектор  называется вектор k
называется вектор k  , удовлетворяющий трем условиям:
, удовлетворяющий трем условиям:
1) k 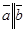 ; 2)
; 2) 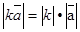 ; 3)
; 3)  и
и 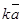
сонаправлены, если k > 0 и противоположно направлены, если k < 0.
Векторы  и
и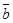 называются противоположными, если
называются противоположными, если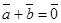 . Для вектора
. Для вектора  противоположным является вектор
противоположным является вектор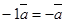 .
.
Линейные операции (сложение, вычитание, умножение вектора на число) над геометрическими векторами обладают свойствами:
1)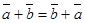 , 2)
, 2)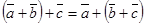 , 3)
, 3)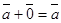 , 4)
, 4)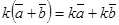 ,
,
5)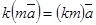 , 6)
, 6)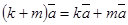 , 7)
, 7)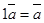 , 8)
, 8)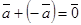 .
.
Основываясь на свойствах линейных операций над геометрическими векторами, переходим к общему определению вектора.
 2014-02-09
2014-02-09 1304
1304