2014-02-09
732
Определение. Множество элементов называется векторным пространством, если для них определено сложение и умножение на число таким образом, что выполняются свойства 1-8, перечисленные выше, при этом элементы этого множества называются векторами.
Это определение очень сильно расширяет представление о векторах. Например, множество всех однотипных матриц, множество всех действительных чисел, множество всех многочленов степени не выше п, множество всех целых чисел, множество всех непрерывных функций и т.д. образуют векторные пространства.
Определение. Если равенство
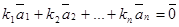
возможно только тогда, когда k1 = k2 = … = kп = 0, то векторы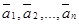 
называются линейно независимыми. Это означает, что ни один из этих векторов нельзя выразить через другие с помощью линейных операций над ними.
Определение. Подмножество векторного пространства называется базисом, если оно состоит из линейно независимых векторов таких, что остальные векторы этого векторного пространства можно выразить через них с помощью линейных операций.
