1. Множество всех векторов, лежащих на прямой, является векторным пространством размерности 1 и обозначается символом R (1). В качестве базиса можно взять любой ненулевой вектор 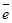 этой прямой, так как для любого вектора
этой прямой, так как для любого вектора  этой прямой найдется единственное число х такое, что
этой прямой найдется единственное число х такое, что 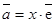 .
.
2. Множество всех векторов, лежащих на плоскости, является векторным пространством размерности 2 и обозначается символом R (2). В качестве базиса можно выбрать любые два неколлинеарные векторы 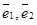 этой плоскости, так как для любого вектора
этой плоскости, так как для любого вектора  этой плоскости найдется единственная пара чисел х1, х2 такая, что
этой плоскости найдется единственная пара чисел х1, х2 такая, что 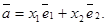
3. Множество всех векторов, лежащих в пространстве, является векторным пространством размерности 3 и обозначается символом R(3). В качестве базиса можно взять любые три вектора 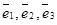 , не лежащие в одной или в параллельных плоскостях, так как для любого вектора
, не лежащие в одной или в параллельных плоскостях, так как для любого вектора  найдется единственная тройка чисел х1, х2, х3 такая, что
найдется единственная тройка чисел х1, х2, х3 такая, что 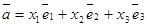 .
.
4. Множество всех квадратных матриц вида 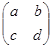 является векторным пространством размерности 4. В качестве базиса можно взять матрицы
является векторным пространством размерности 4. В качестве базиса можно взять матрицы
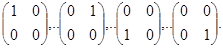
В этом случае числа а, b, с, d являются координатами вектора матрицы 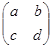 , так как
, так как
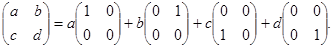
 2014-02-09
2014-02-09 1047
1047
