Задача. Найти координаты вектора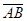 , если A(x1;y1), В(х2у2) – точки, координаты которых известны.
, если A(x1;y1), В(х2у2) – точки, координаты которых известны.
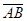 =
= 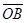 -
- 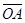 = (x
= (x 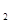
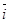 + у
+ у 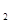
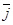 ) - (x
) - (x 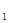
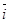 + y
+ y 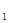
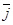 ) =
) =
= (x 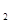 -x
-x 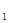 )
) 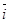 +(y
+(y 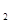 -y
-y 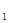 )
) 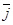 .
.
Таким образом, для получения координат вектора 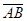 надо из координат конца вычесть соответствующие координаты начала. Это правило справедливо и для векторов в системе координат xoyz.
надо из координат конца вычесть соответствующие координаты начала. Это правило справедливо и для векторов в системе координат xoyz.
Задача. Найти длину вектора, если координаты х и у известны.
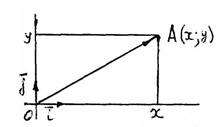
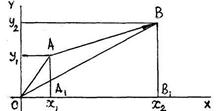
Решение. Так как вектор  можно отождествить с вектором – диагональю прямоугольника, стороны которого совпадают с векторами – сторонами
можно отождествить с вектором – диагональю прямоугольника, стороны которого совпадают с векторами – сторонами 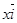 и
и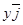 , то
, то
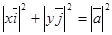 , или
, или 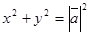 .
.
Следовательно,
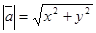 .
.
Таким образом, длина вектора равна квадратному корню из суммы квадратов его координат. Этот вывод верен для вектора 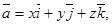 т. е.
т. е. 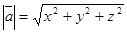 .
.
Задача. Найти координаты точки M(x;y), делящей отрезок M1(x1;y1)M2(x2;y2) в отношении 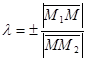 , где знак «+» выбирается, если М лежит на отрезке М1М2 и знак "- " выбирается, если М лежит на продолжении отрезка М1М2.
, где знак «+» выбирается, если М лежит на отрезке М1М2 и знак "- " выбирается, если М лежит на продолжении отрезка М1М2.
 2014-02-09
2014-02-09 736
736








