Декартовы координаты вектора и их свойства

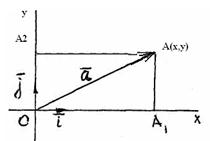
Пусть 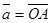- вектор, расположенный в декартовой системе координат хоу. Найдем его декартовы координаты.

Для этого спроецируем точку А наоси координат и получим точки А₁ и А₂. Величины направленных отрезков 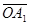и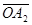осей координат являются проекциями вектора на оси координат и совпадают с координатами х и у точки А, т.е. 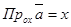,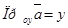. Следовательно, 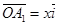,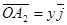. Из прямоугольника ОА₁АА₂ по правилу параллелограмма имеем: .

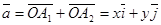Таким образом, координаты вектора в декартовом базисе можно отождествлять с проекциями вектора на оси координат. Это верно и для вектора в базисе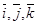. Из этого следует, что при сложении, вычитании векторов надо складывать, вычитать соответствующие координаты, а при умножении вектора на число надо каждую координату умножать на это число.