Пусть 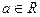 - точка сгущения множества
- точка сгущения множества 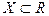 . Тогда она является точкой сгущения, по крайней мере, одного из множеств
. Тогда она является точкой сгущения, по крайней мере, одного из множеств
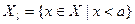
и
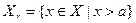
Вместе с тем, точкой сгущения обоих этих множеств, одновременно, она может и не быть, так как одно из них может быть, например, пустым.
Пусть 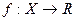 . Положим
. Положим 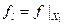 и
и 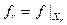 .
.
Определение 1. Пусть 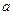 - точка сгущения множества
- точка сгущения множества 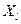 (соотв.,
(соотв., 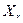 ). Если существует предел
). Если существует предел 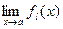 (соотв.,
(соотв., 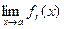 ), то он называется левосторонним (соотв., правосторонним) пределом функции
), то он называется левосторонним (соотв., правосторонним) пределом функции  в точке
в точке 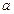 , или также пределом функции
, или также пределом функции 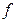 при
при 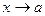 слева (соотв., при
слева (соотв., при 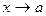 справа).
справа).
В отличие от левостороннего и правостороннего пределов «обычный» предел функции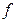 при
при 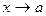 называется иногда двусторонним.
называется иногда двусторонним.
Левосторонний предел функции 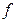 в точке
в точке 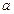 обозначается обычно одним из символов
обозначается обычно одним из символов
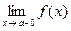 или
или 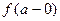 ,
,
а правосторонний, соответственно, – одним из символов
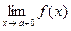 или
или 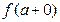 ..
..
Замечание 1. Поскольку односторонние пределы являются в то же время и обычными пределами, то для них справедливы все теоремы, которые устанавливаются для обычных двусторонних пределов.
Теорема 1. Пусть 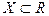 ,
, 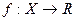 и
и 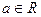 – точкасгущения каждого из множеств
– точкасгущения каждого из множеств 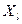 и
и 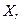 . Тогда, если существуют равные между собой односторонние пределы
. Тогда, если существуют равные между собой односторонние пределы 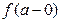 и
и 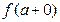 , то существует и равный им двусторонний предел
, то существует и равный им двусторонний предел
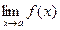 =
=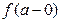 =
=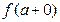 .
.
Д о к а з а т е л ь с т в о. Прежде всего заметим, что пересечение любых двух окрестностей точки 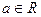 является окрестностью этой точки.
является окрестностью этой точки.
Пусть
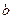 =
= 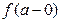 =
=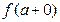
и 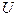 - произвольная окрестность точки
- произвольная окрестность точки 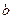 .
.
По определению 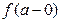 имеем:
имеем: 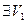 - окрестность точки точки
- окрестность точки точки 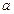 такая, что
такая, что
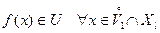 | (1) |
Аналогично, по определению 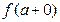 имеем:
имеем: 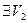 - окрестность точки
- окрестность точки 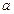 такая, что
такая, что
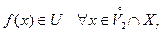 | (2) |
Рассмотрим теперь следующую окрестность точки 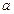 :
: 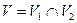 . Очевидно,
. Очевидно,
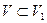 и
и 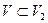 .
.
Следовательно,
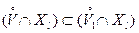 ,
,
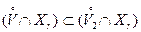
и, кроме того, ясно, что
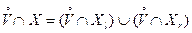 .
.
Поэтому из (1) и (2) следует, что

В силу произвольности выбранной окрестности 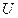 точки
точки 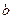 , это и означает, что
, это и означает, что 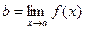 □
□
§4. Расширение понятия предела: бесконечные пределы и пределы в бесконечности
Определения. 1. Окрестностью точки 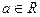 в
в 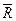 называется всякое множество
называется всякое множество 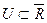 , которое содержит некоторую
, которое содержит некоторую 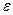 -окрестность
-окрестность 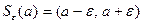 этой точки.
этой точки.
2. Окрестностью точки 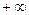 в
в 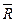 называется любой промежуток вида
называется любой промежуток вида 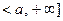 , где
, где 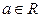 .
.
3. Окрестностью точки 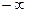 в
в 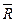 называется любой промежуток вида
называется любой промежуток вида 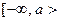 , где
, где 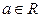 .
.
4. Пусть 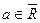 и
и 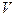 –окрестность этой точки (в
–окрестность этой точки (в 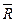 ). Тогда множество
). Тогда множество
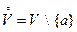
называется проколотой окрестностью точки 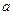 .
.
5. Точка 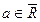 называется точкой сгущения множества
называется точкой сгущения множества 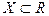 , если для любой окрестности
, если для любой окрестности 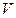 этой точки
этой точки
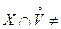 Æ.
Æ.
Теперь естественным образом можно расширить понятие предела 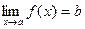 для случая, когда обе или одна из точек
для случая, когда обе или одна из точек 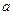 и
и 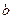 являются бесконечными точками расширенной числовой оси
являются бесконечными точками расширенной числовой оси 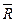 . Соответствующее определение почти дословно повторяет определение 2” из §1.
. Соответствующее определение почти дословно повторяет определение 2” из §1.
Определение 6. Пусть 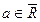 – точка сгущения множества
– точка сгущения множества 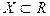 и функция
и функция  определена на множестве
определена на множестве 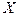 . Конечное или бесконечное число (точка)
. Конечное или бесконечное число (точка) 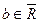 называется пределом функции
называется пределом функции 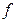 при
при 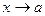 (или в точке
(или в точке 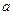 ), если для любой окрестности
), если для любой окрестности 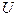 точки
точки 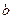 (в
(в 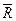 ) существует такая окрестность
) существует такая окрестность 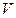 точки
точки 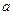 (в
(в 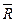 ), что
), что
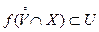 .
.
Замечание 1. Для различных типов точек 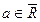 и
и 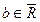 определение 5 можно детализировать с учетом определения окрестностей для соответствующих типов точек. Например, равенство
определение 5 можно детализировать с учетом определения окрестностей для соответствующих типов точек. Например, равенство 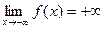 означает, что
означает, что 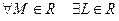 такое, что
такое, что 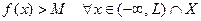 .
.
Упражнение 1. По аналогии с тем, как это сделано в замечании 2, сформулировать, что означает
А) 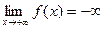 ,
,
Б) 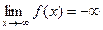 ,
,
В) 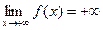 ,
,
Г) 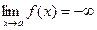 (
(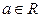 ),
),
Д) 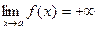 (
(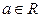 ),
),
Е) 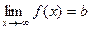 (
(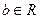 ),
),
Ж) 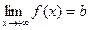 (
(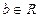 ).
).
Замечание 2. Если существуют пределы функции 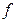 как при
как при 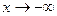 , так и при
, так и при 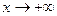 , причем
, причем
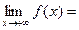
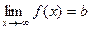 ,
,
то пишут
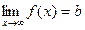 .
.
 2014-02-09
2014-02-09 1490
1490
