Точки разрыва функции. Классификация точек разрыва.
.
Как будет показано далее все элементарные функции являются непрерывными в своих областях определения. В связи с этим напомним, что к числу, так называемых, основных элементарных функций относятся:
– постоянная функция: 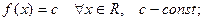
– степенная функция: 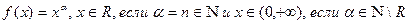 ;
;
– показательная функция: 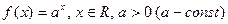 ;
;
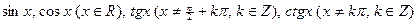 ;
;
– обратные тригонометрические функции:
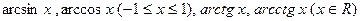 .
.
В свою очередь, элементарной называется всякая функция, которая может быть получена из основных элементарных функций с помощью конечного числа арифметических операций и образования суперпозиций.
Теорема 1 (О непрерывности сужения). Пусть функция 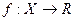 непрерывна в точке
непрерывна в точке 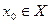 и
и 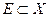 причем
причем 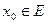 . Тогда функция
. Тогда функция 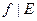 также непрерывна в точке
также непрерывна в точке  .
.
Д о к а з а т е л ь с т в о вытекает из определения сужения и определения непрерывности.
Теорема 2 (Арифметические свойства непрерывных функций). Пусть функции  и
и 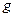 определены на множестве
определены на множестве 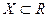 и непрерывны в точке
и непрерывны в точке 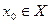 . Тогда и функции:
. Тогда и функции:
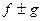 ,
, 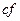
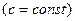 ,
, 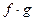 ,
, 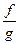 (при
(при 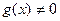 на
на 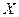 )
)
непрерывны в точке  .
.
Теорема 3 (О локальной ограниченности). Пусть функция  определена на множестве
определена на множестве 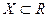 и непрерывна в точке
и непрерывна в точке 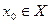 . Тогда существует такая окрестность
. Тогда существует такая окрестность 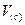 точки
точки  , что функция
, что функция  ограничена на множестве
ограничена на множестве 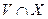 .
.
Теорема 4 (О стабилизации знака). Пусть функция  определена на множестве
определена на множестве 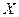 и непрерывна в точке
и непрерывна в точке 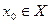 . Тогда если
. Тогда если 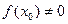 , то существует такая окрестность
, то существует такая окрестность 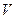 точки
точки  , что
, что 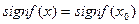
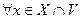 .
.
Наконец отметим еще две простые теоремы
Теорема 5. Пусть функция 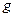 определена на множестве
определена на множестве 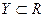 и непрерывна в точке, а функция
и непрерывна в точке, а функция определена на множестве
определена на множестве 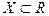 и непрерывна в точке
и непрерывна в точке 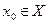 , причем
, причем 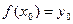 и
и 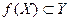 . Тогда сложная функция
. Тогда сложная функция 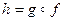 непрерывна в точке
непрерывна в точке  .
.
Д о к а з а т е л ь с т в о. Выберем произвольную последовательность 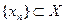 ,
, 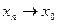 . Так как
. Так как  - непрерывна в точке
- непрерывна в точке  , то
, то
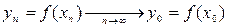 ,
,
а так как 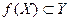 , то
, то 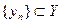 . Поэтому, в силу непрерывности функции
. Поэтому, в силу непрерывности функции 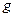 в точке
в точке 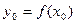 , имеем
, имеем
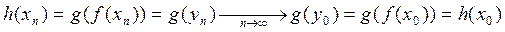 ,
,
то есть
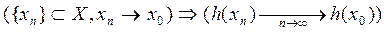 ,
,
что и означает, что функция 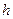 - непрерывна в точке
- непрерывна в точке  .
.
Пусть функция  определена на множестве
определена на множестве 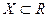 и
и 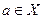 . Рассмотрим множества:
. Рассмотрим множества:
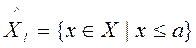
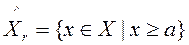
Определение 1. Функция  называется непрерывной слева (непрерывной справа) в точке
называется непрерывной слева (непрерывной справа) в точке 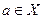 , если функция
, если функция 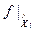 (соответственно
(соответственно 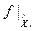 ) непрерывна в точке
) непрерывна в точке 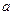 .
.
Замечание. На языке 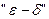 определение, например, непрерывности слева, формулируется следующим образом: функция
определение, например, непрерывности слева, формулируется следующим образом: функция 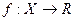 называется непрерывной слева в точке
называется непрерывной слева в точке 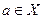 , если
, если 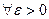
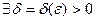 такое, что
такое, что 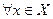 удовлетворяющего неравенствам
удовлетворяющего неравенствам
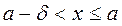
справедливо неравенство
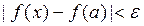 .
.
Теорема 6. Функция 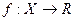 непрерывна в точке
непрерывна в точке 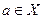
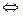 она непрерывна в ней слева и справа одновременно.
она непрерывна в ней слева и справа одновременно.
Если 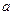 - изолированная точка множества
- изолированная точка множества 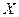 , то утверждение очевидно. Если же
, то утверждение очевидно. Если же 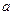 - точка сгущения множества
- точка сгущения множества 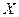 , то оно вытекает из аналогичной теоремы об односторонних пределах.
, то оно вытекает из аналогичной теоремы об односторонних пределах.
Определение 1. Пусть функция  определена на множестве
определена на множестве 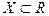 и
и 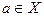 . Если функция
. Если функция  непрерывна в точке
непрерывна в точке 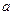 , то она называется точкой непрерывности функции
, то она называется точкой непрерывности функции  . В противном случае, точка
. В противном случае, точка 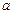 называется точкой разрыва функции
называется точкой разрыва функции  .
.
Замечание 1. Так как всякая изолированная точка множества 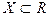 является точкой непрерывности определенной на нем функции
является точкой непрерывности определенной на нем функции  , то точками разрыва могут быть только точки сгущения множества
, то точками разрыва могут быть только точки сгущения множества 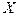 .
.
Замечание 2. Если 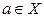 – точка разрыва функции
– точка разрыва функции 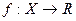 , то либо предел
, то либо предел 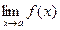 не существует, либо он существует, но
не существует, либо он существует, но 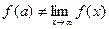 .
.
Определение 2. Точка разрыва 1-го рода называется точкой устранимого разрыва функции  , если в ней существует предел функции
, если в ней существует предел функции  , но он не равен ее значению в этой точке.
, но он не равен ее значению в этой точке.
Замечание 4. Если точка 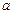 – точка устранимого разрыва функции
– точка устранимого разрыва функции  , то изменив ее значение в этой точке на значение, равное величине предела в этой точке, получим непрерывную функцию в этой точке
, то изменив ее значение в этой точке на значение, равное величине предела в этой точке, получим непрерывную функцию в этой точке
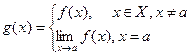 .
.
Этим и объясняется термин точка устранимого разрыва.
В следующих двух определениях предполагается, что точка 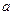 принадлежит области определения функции
принадлежит области определения функции 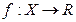 вместе с некоторой своей окрестностью
вместе с некоторой своей окрестностью 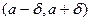 .
.
Определение 3. Пусть 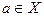 – точка разрыва функции
– точка разрыва функции 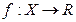 . Если оба односторонних предела
. Если оба односторонних предела 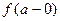 и
и 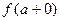 существуют и конечны, то она называется точкой разрыва 1-го рода
существуют и конечны, то она называется точкой разрыва 1-го рода
Определение 4. Точка разрыва функции называется точкой разрыва 2-го рода, если она не является точкой разрыва 1-го рода.
Замечание 3. Иными словамиточка разрыва функции является точкой разрыва 2-го рода, если в ней хотя бы один из односторонних пределов не существует, либо является бесконечным.
Проиллюстрируем данные выше определения на некоторых примерах.
Пример 1 (всюду разрывной функции). Функция Дирихле, определенная на всей числовой оси равенствами:
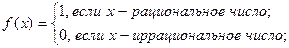
является разрывной в каждой точке 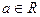 . Действительно, для любой последовательности рациональных чисел
. Действительно, для любой последовательности рациональных чисел 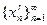 , сходящейся к точке
, сходящейся к точке 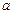 , имеем
, имеем 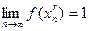 , а для любой последовательности иррациональных чисел
, а для любой последовательности иррациональных чисел 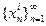 ,
, 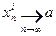 , в свою очередь, имеем
, в свою очередь, имеем 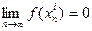 . Следовательно, ни в одной точке
. Следовательно, ни в одной точке 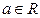 не существует предел
не существует предел 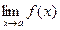 и, следовательно каждая точка
и, следовательно каждая точка 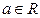 – точка разрыва функции Дирихле. Более того, нетрудно видеть, что ни в одной точке
– точка разрыва функции Дирихле. Более того, нетрудно видеть, что ни в одной точке 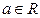 не существуют оба односторонних придела
не существуют оба односторонних придела 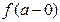 и
и 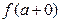 , так как описанные выше последовательности
, так как описанные выше последовательности 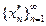 и
и 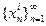 , с одной стороны, можно выбрать так, что
, с одной стороны, можно выбрать так, что 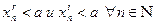 , а с другой стороны, можно выбрать и так, что
, а с другой стороны, можно выбрать и так, что 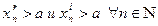 . Таким образом, каждая точка
. Таким образом, каждая точка 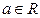 – точка разрыва 2-го рода функции Дирихле.
– точка разрыва 2-го рода функции Дирихле.
Пример 2. Функция «сигнум 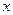 »
»
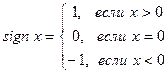
очевидно, разрывна в точке 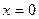 , причем эта точка – точка разрыва 1-го рода.
, причем эта точка – точка разрыва 1-го рода.
Пример 3. Функция 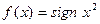 разрывна в точке
разрывна в точке 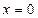 , которая, очевидно, является точкой устранимого разрыва.
, которая, очевидно, является точкой устранимого разрыва.
Определение 1. Функция  называется равномерно непрерывной на множестве
называется равномерно непрерывной на множестве 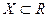 , если для любого
, если для любого 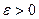
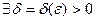 такое, что
такое, что 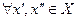 , удовлетворяющих неравенству
, удовлетворяющих неравенству
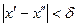 | (1) |
имеет место неравенство
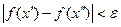 . . | (2) |
Замечание 1. Очевидно, если функция  равномерно непрерывна на множестве
равномерно непрерывна на множестве 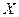 , то она и непрерывна на нем, т.е. непрерывна в каждой точке этого множества. Как показывает приводимый ниже пример, обратное утверждение, вообще говоря, неверно, т.е. из непрерывности функции
, то она и непрерывна на нем, т.е. непрерывна в каждой точке этого множества. Как показывает приводимый ниже пример, обратное утверждение, вообще говоря, неверно, т.е. из непрерывности функции  на множестве
на множестве 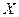 , вообще говоря, не следует, что она равномерно непрерывна на этом множестве.
, вообще говоря, не следует, что она равномерно непрерывна на этом множестве.
Пример 1. Функция
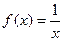
непрерывна на множестве 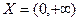 . Покажем, что она не является равномерно непрерывной на нем. Предположим противное, т.е. что она все же является равномерно непрерывной на множестве
. Покажем, что она не является равномерно непрерывной на нем. Предположим противное, т.е. что она все же является равномерно непрерывной на множестве 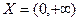 . Тогда
. Тогда 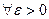
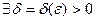 такое, что при
такое, что при
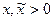 , , 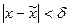 , , | (3) |
будет справедливо неравенство
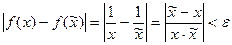 . . | (4) |
Пусть 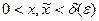 . Тогда условия (3) выполнены и, следовательно, имеет место неравенство (4). Это неравенство, в частности показывает, что при фиксированном
. Тогда условия (3) выполнены и, следовательно, имеет место неравенство (4). Это неравенство, в частности показывает, что при фиксированном  ,
, 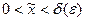 функция
функция
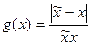
ограничена на интервале 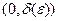 . Но это противоречит тому, что
. Но это противоречит тому, что 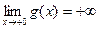 . Таким образом, непрерывная на множестве
. Таким образом, непрерывная на множестве 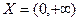 функция
функция 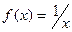 не является равномерно непрерывной на этом множестве.
не является равномерно непрерывной на этом множестве.
Замечание 2. Отличие понятия равномерно непрерывной на множестве 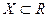 функции от понятия непрерывной на нем функции состоит в том, что если функция
функции от понятия непрерывной на нем функции состоит в том, что если функция  – непрерывна на множестве
– непрерывна на множестве 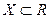 , то для каждой точки
, то для каждой точки 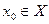 и для каждого
и для каждого 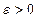 существует свое, т.е. зависящее и от
существует свое, т.е. зависящее и от 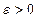 , и от точки
, и от точки 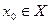 число
число 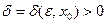 , которое для всех
, которое для всех 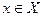 , удовлетворяющих неравенству
, удовлетворяющих неравенству
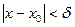 , , | (5) |
гарантирует выполнение неравенства
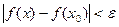 . . | (6) |
Если же функция  – равномерно непрерывна на множестве
– равномерно непрерывна на множестве 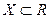 , то для каждого
, то для каждого 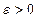 независимо от выбора точки
независимо от выбора точки 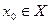 существует зависящее только от выбранного
существует зависящее только от выбранного 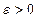 число
число 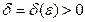 , которое для всех
, которое для всех 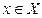 , удовлетворяющих неравенству (5), гарантирует выполнение неравенства (6).
, удовлетворяющих неравенству (5), гарантирует выполнение неравенства (6).
Следующая теорема указывает тот важный, частный случай, когда из непрерывности функции  на множестве
на множестве 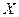 следует также и ее равномерная непрерывность на том же множестве.
следует также и ее равномерная непрерывность на том же множестве.
Теорема 1 (Кантора). Непрерывная на отрезке 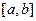 функция
функция  равномерно непрерывна на этом отрезке.
равномерно непрерывна на этом отрезке.
Д о к а з а т е л ь с т в о. Предположим противное. Пусть функция  непрерывна на отрезке
непрерывна на отрезке 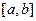 , но не является равномерно непрерывной на нем. Тогда существует такое
, но не является равномерно непрерывной на нем. Тогда существует такое 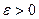 , что для любого
, что для любого 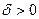 найдутся такие точки
найдутся такие точки 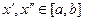 ,
, 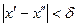 , что
, что
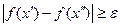
Рассмотрим последовательность 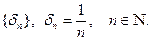 . Тогда, в соответствии со сказанным выше, для любого
. Тогда, в соответствии со сказанным выше, для любого 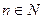 найдутся такие
найдутся такие 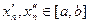 , что наряду с неравенством
, что наряду с неравенством
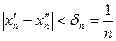 | (7) |
имеет место и неравенство
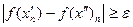 . . | (8) |
Так как 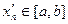
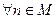 , то последовательность
, то последовательность 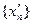 ограничена. Тогда по теореме Больцано-Вейерштрасса из нее можно выделить сходящуюся подпоследовательность
ограничена. Тогда по теореме Больцано-Вейерштрасса из нее можно выделить сходящуюся подпоследовательность 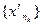 . Пусть
. Пусть 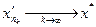 . Очевидно
. Очевидно 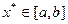 . Рассмотрим последовательность
. Рассмотрим последовательность 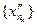 и покажем, что
и покажем, что 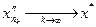 . Действительно, в силу неравенства (7) и определения подпоследовательности имеем
. Действительно, в силу неравенства (7) и определения подпоследовательности имеем
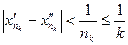
и, следовательно,
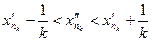 .
.
Поэтому в силу того, что
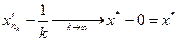 и
и 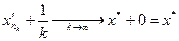 ,
,
по принципу двух милиционеров имеем 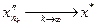 .
.
Так как функция  непрерывна на отрезке
непрерывна на отрезке 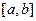 , и, стало быть – и в точке
, и, стало быть – и в точке 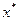 , а
, а
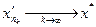 и
и 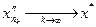 ,
,
то
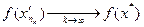 и
и 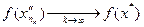 .
.
Учитывая теперь, что из неравенства (8) вытекает неравенство
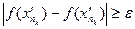 , и переходя в последнем неравенстве к пределу при
, и переходя в последнем неравенстве к пределу при 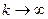 , получим
, получим 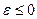 , что противоречит выбору
, что противоречит выбору 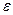 □
□
Колебанием функции  на отрезке
на отрезке 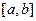 называется величина
называется величина
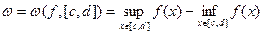 .
.
Нетрудно убедиться, что
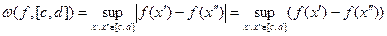 | (9) |
С учетом равенств (9) легко доказать, что справедлива следующая
Теорема 2. Для того, чтобы функция  была равномерно непрерывной на отрезке
была равномерно непрерывной на отрезке 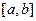 необходимо и достаточно, чтобы для любого
необходимо и достаточно, чтобы для любого 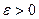 существовало такое
существовало такое 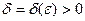 , что для любого отрезка
, что для любого отрезка 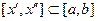 длиной меньшей
длиной меньшей 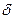
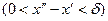 колебание функции
колебание функции  на этом отрезке было меньше
на этом отрезке было меньше 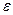 , т.е.
, т.е. 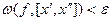 .
.
Еще один критерий равномерной непрерывности можно сформулировать в терминах так называемого модуля непрерывности функции  : модулем непрерывности функции
: модулем непрерывности функции  , определенной на множестве
, определенной на множестве 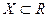 называется определенная при
называется определенная при 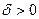 функция
функция
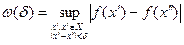 .
.
Теорема 3. Для того, чтобы функция  была равномерно непрерывной на множестве
была равномерно непрерывной на множестве 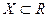 , необходимо и достаточно, чтобы ее модуль непрерывности на этом множестве стремился к нулю при
, необходимо и достаточно, чтобы ее модуль непрерывности на этом множестве стремился к нулю при 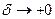 , т.е.
, т.е.
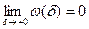
 2014-02-09
2014-02-09 6033
6033

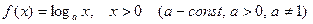 ;
;